
It is easy to see from the equation (*) above that:
It is possible to extend the lines CF and BE until they intersect the
line through point A that is parallel to the line BC at H and I.
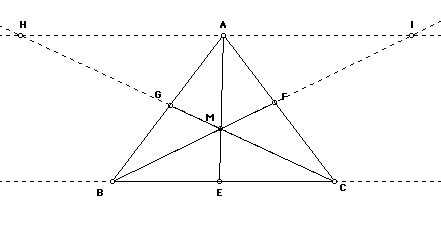
Several similar triangles can now be recognized such as: AGH ~ BGC ,
AFI ~ CFB , AMI ~ EMB, AMH ~ EMC. We can conclude that from AGH ~ BGC that
AG/GB = AH/BC and from AFI ~ CFB that AF/FC = AI/BC. Also, AMI ~ EMB shows
that AI/BE = AM/ME and AMH ~ EMC shows that AH/EC = AM/ME. Therefore we
know that AI/BE = AH/ EC which gives us that BE/EC = AI/AH.
Then by multiplying the proportions of the sides of triangle ABC we find:
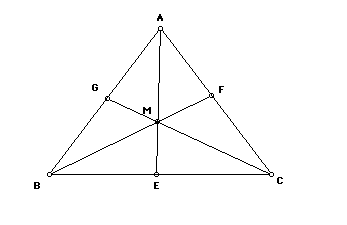
Therefore the statement holds that if given triangle ABC, three lines
AE, BF, CG intersect at a single point M, then (AG/BG)(BE/CE)(CF/AF) = 1.
It is left to prove the theorem in the other direction. Assume M is the
point where AE and CG intersect, then draw a line from B through M to line
AC at point F '. So we have
(AG/GB)(BE/EC)(CF '/F 'A) = 1 , but we assumed that (AG/GB)(BE/EC)(CF/FA)
= 1.
This implies that CF' '/ F 'A = CF/FA. We can add a 1 to both sides to get
CF '/F 'A + 1 = CF/FA +1. So (CF ' + F 'A)/ F 'A = (CF + FA)/FA. From this
it is easy to see that CA/F 'A = CA / FA implies (F 'A)(CA) = (CA)(FA) or
F 'A= FA. Therefore F= F '. So we can conclude that if
(AG/BG)(BE/CE)(CF/AF) = 1 then lines AE, BF, and CG intersect at a single
unique point.
The following statements can be investigated using GSP. Explore by changing
the position of the points A,B,&C to see that the theroem still holds.
From this theorem it follows that the medians of a triangle intersect at
a single point which is named the centroid.
We can verify that (AG/BG)(BE/CE)(CF/AF) = 1.
It also follows that the altitudes of a triangle intersect at a single point,
the orthocenter.The
right triangles AEC and BCF are similar triangles. Therefore, we know that
CE/CF = BF/AE. Similarly, BE/BG = AE/CG and AG/AF = BF/CG. Then using Ceva's
Theorem (AG/BG)(BE/CE)(CF/AF) = 1 we can rearrange our proportions to read
(AG/AF)(BE/BG)(CF/CE)=1. Finally we can substitute our values from the beginning
assumptions to get (BF/CG)(CG/AE)(AE/BF) which all cancels out to equal
1.
We can also conclude that the angle bisectors of a triangle all intersect
at one point, the incenter.
Because AE, BF, and CG are angle bisectors we know that (AG/GB) = (AC/BC),
(BE/EC) = (AB/AC) , and (AF/FC) = (AB/CB). We can then multiply these ratios
together. Using Ceva's theorem the first proportion of each equality multiplied
together equals one. The remaining proportions all cancel out to equal one.
Therefore we have that the angle bisectors intersect at one point.
Finally, Ceva's Theorem also implies that the perpendicular bisectors of
a triangle all intersect at a single point, the circumcenter.
The proof is similar to the above mentioned. It is easy to see that because
BF, GC, EA are perpendicular bisectors then we know they AF=FC and so forth.
Therefore, the theorem holds.
The investigations that I have done have all be dependent on the intersecton
of the point inside the triangle. I encourage you to investigate the Ceva's
Theorem when the intersection point is on one of the edges of the triangle
or outside the triangle. Does the theorem still hold? It is also interesting
to compare the proofs of the intersection point in a direct way as compared
to using Ceva's Theorem.
Return to Heather's Home Page.