Pick's and Euler's Theorems

By: Heather Bridges

If we begin with Pick's Formula which is that the area of a lattice polygon with interior points (I) and border points (B) can be represented by the formula.

We are going to derive Euler's Formula for a lattice polygon which is in terms of the edges (E), faces (F), and vertices (V). Let's begin by constructing and triangulating several lattice polygons. Then count the number of interior points, border points, faces, and vertices.

From this we can deduuce that V = B + I. The triangulated polygons are all seperated into fundamental triangles ( B=3, I=0) so

We can use this to find the relationship of F to B and I. We know that

Set these formulas equal to each other and solve for F which leaves F = B + 2I - 2.

Now let's go back to investigate polygons in terms of the edges by susequently keeping B constant and increasing I by 1.

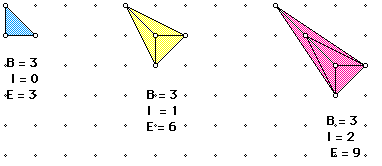
Therefore we can deduce that E = B + 3 I when B remains constant. Then keep I constant and subsequently increase B by one.

So E = 2 B - 3 when I remains constant. We can then analyze our formulas to discover that
E = 2B + 3I - 3.

Now to gather all the formulas we have discovered:

So E = 2 B + 3 I - 3 = B + 2 I - 2 + B + I then we can substitute our formulas for F & A to get the following:

Euler's Formula E = V + F - 1.

It is also easy to now work backwards from Euler's Formula to derive Pick's Formula.

It is also interesting to try to develop Pick's Formula from only using the characteristics of a fundamental triangle and expanding on that. I encourage readers to do so.

Return to Heather's Homepage.