
Transformational Geometry
by:
Heather Bridges
&
Leanne May
Day 1:
Goal: For the students to recognize the terms and understand the properties
of basic mappings.
Pre-requisite knowledge: We expect the students to have studied the
properties of congruent and similar figures and one-to-one correspondences
between geometric figures.
Open discussion and lecture material:
We are going to look at the effects on figures when they are moved around
in a plane. These motions are described mathematically as coorespondences
between sets of points called mappings. A correspondance between sets P
and Q is a mapping of P to Q if and only if each member of P corresponds
to one and only one member of Q.
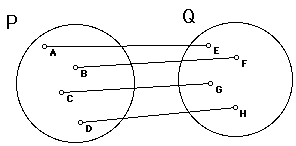
Mappings are usually expressed in the form F : P -> Q which represents
a mapping from set P to set Q. In the case above, E is called the image
of A under mapping F and A is called the preimage of E. The above mapping
is also termed one-to-one because every image in Q has exactly one preimage
in P. A mapping is a transformation if and only if it is a one-to-one mapping
of the plane onto itself. So transformations are the correspondence of points
in a plane. They are usually defined as mappings of the entire plane to
itself but we are going to focus on mappings of geometric figures because
it is more interesting. The points in a plane are referred to as ordered
pairs (x,y). When we are working with mappings of geometric figures it is
important that our transformations preserve the distance between points
in a plane. These types of transformations are called isometries or a congruence
mapping. There are also so mappings that increase or decrease the distance
between points in proportion to the original figure.
The students will then be asked to do several examples and problems in the
book to practice working with mapping.
Day 2:
Goal: For the students to locate images of figures by reflections.
Open discussion and lecture: When you look in mirrors and in pools you see
your reflection. An object and its reflected image can be described mathematically
using a geometric transformation called a reflection.. When you look
at yourself in the mirror your reflection appears to be as far in "back"
of the mirror as you are in "front". If you were to reflect an
object in the mirror then you can think of it as the perpendicular bisector
of the segments connecting corresponding points of the object and its image.
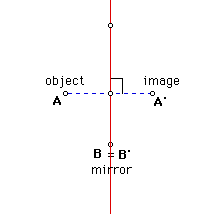
Then we will give the students the definition of reflection. Definition:
A transformation is a reflection in line l if and only if
the following conditions are satisfied:
a. if A is a point of l , then the image of A is A;
b. if A is not on l , then the image of A is A' , such that l
is a perpendicular bisector of the segment AA'.
Geometric figures can be reflected in a line by reflecting each point
or enough points to determine the figure. Observe that reflection in a line
preserves betweeness of points, collinearity, angles, angle measure, and
segment length. This theorem, a reflection in a line is an isometry, verifies
that reflection preserves distance between points.
Then we will go over several examples of reflections.
We will also show them an example on GSP of a reflection.
For homework the students will do problems from the book to turn in the
following day.
Day 3:
Goal: For the students to locate and understand images of figures by
rotations.
Class discussion and lecture material:
Can anyone give me some examples of rotations?
A transformation is a rotation having a center C and angle measure
a if and only if each point P in the plane is associated with point P '
such that:
i. If P is different from C, then CP = CP ' and m<PCP ' = a.
ii. C is a fixed point.
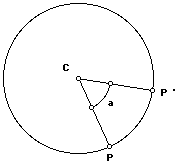
If (a) is a positive angle measure, the rotation is counterclockwise.
If (a) is negative, the rotation is clockwise.
Theorem : A rotation is an isometry. Other than the distance between points,
rotations do a lot more. They preserve betweeness, collinearity, angles
and their measures, segments, rays, and lines.
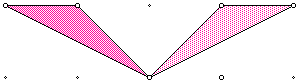
The following is an example of a rotation of a geometric figure.
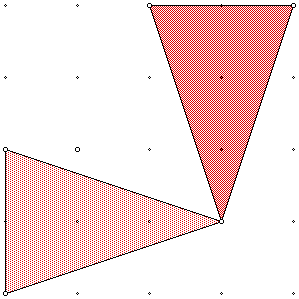
We will do several examples with the class and show them the following
example in GSP of a rotation.
The students will then have homework that reinforces their understanding
of rotations.
Day 4:
Goal: For the students to be able to construct their own examples of
rotations and reflections on GSP.
Open discussion and lecture: The students will construct examples of rotations
and reflections on GSP. We will give a brief explanation of how to rotate
and reflect on GSP. Although we expect the students to be very familiar
with GSP. They will be responsible to make their own figures and if time
permits display them for the class and explain what they did and what is
happening in their picture.
Day 5:
Goal: For the students to use vectors to represent translations and
to locate images of figures by translations and glide reflections.
Open discussion and lecture: First we will apply translations to real life
applications. Sliding down a sliding board or gliding on ice illustrates
real life translations. Then we will see if the students can discover other
real life applications that illustrate translations.
For our first example: If a triangle ABC glides along the path indicated
by the arrow, the triangle DEF will coincide with triangle D'E'F''. This
motion describes a transformation of the plane called a translation
. A translation glides all points of a plane the same distance and
in the same direction . Arrows called vectors indicate the
distance and direction of the glide. Vector AA' is shown in this figure.
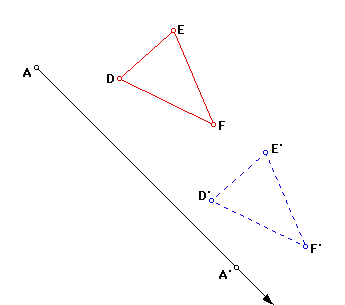
Now give the definition: If A and B are points, and A' and B' are their
images under a transformation T, then T is a translation if and only if:
a. AA' = BB'
b. segment AA' || segment BB'
c. segment AB || segment A'B'
Then we will see if the students can determine what these conditions
verify. They should determine that condition (a) verifies that all points
of the plane are glided the same distance under a translation. Conditions
(b) and (c) guarantee that points are glided in the same direction
. They should also notice that under these conditions that AA'BB' is a parallelogram.
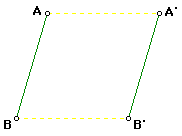
Hence AB = A'B'. Thus a translation is an isometry. Now we will
look at some examples of translations using the coordinate plane.
We will also show the students an example on GSP of translations.
For homework the students will do a worksheet containing all the material
we have already taught.
Day 6:
Goal: For the students to locate images of figures by dilations.
Class discussion and lecture material:
Some transformations project the images in proportion to the original figure.
These transformations that result in size changes are called dilations.
A dilation has a center and a nonzero scale factor.
A transformation is a dilation with center O and scale factor k if
and only if each point P maps to a point P ' such that:
i. If k > 0, P ' is on the ray OP and OP ' = k * OP.
ii. If k < O, P ' is on the ray opposite the ray OP and OP ' = |k| *
OP.
iii. O is a fixed point.
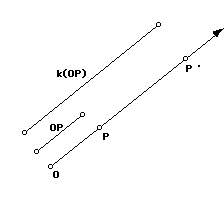
If |k| > 1, the dilation is an expansion of the original figure. If
|k| < 1 the dilation is a contraction.
The dilation maps every line segment to a parallel line segment that is
|k| times as long.
We will show the students the following example of the dilation of a geometric
figure.
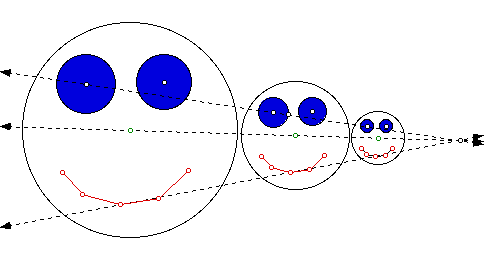
There is also a clever diplay using GSP that could help the students
to better understand the concept of dilations.
The students will then be given a homework assignment.
Day 7:
Goal: For the students to be able to construct their own examples of
translations and dialations on GSP.
Open discussion and lecture: The students will construct examples of translations
and dialations on GSP. We will give a brief explanation of how to translate
and dialate on GSP. The students have already worked with rotating and reflecting
objects on GSP so they should be familiar with the basics of working with
these applications. They will be responsible to make their own figures and
if time permits display them for the class and explain what they did and
what is happening in their picture.
Day 8:
Goal: For the students to be able to work with Tesselmania and see how
these ridiged motions tie in with tesslations.
Open discussion and lecture: The students will be given a small lecture
on tessellations. We will show the students how the ridiged motions we have
been teaching tie in with tessellations. The program Tesselmania allows
the students to be creative and come up with their own patterns of tessellations.
We will let the students work on the program the remainder of the period
and see what creations they can produce like the following:

Day 9 :
Goal: To locate the images of figures by a compostion of mappings.
Class discussion and lecture material:
Explanation will be given on how transformations can be carried out in succession.
For instance we can the same figure about two different lines.
We will give explanation of the following theorems :
Theorem: The composition of two isometries is an isometry.
Theorem: A composition of reflections in two parallel lines is a
translation. The translation glides all points through twice the distance
between the lines.
Theorem: A composition of reflections in two intersecting lines is
a rotation about the point of intersection of the two lines. The measure
of the angle of rotation is twice the measure of the angle from the first
line of reflection to the second.
Corollary: A composition of reflections in perpendicular lines is
a half-turn about the point where the lines intersect.
The students will be given classwork to practice with the compositions of
mapping.
We will also give a homework sheet to review for the test tomorrow.
Day 10:
Goal: For the students to display their knowledge over the material we have
taught them.
We will give the students a test over Transformational Geometry. They will
not only have to recall the definitions, work general problems, but will
be responsible to create these different types of ridiged motions on GSP.
Therefore the students need to be familiar with the program.
Return to Heather's Home
Page











