The

Golden Cut

of a

Segment

by Teresa Banker

The problem of finding the golden section of a segment is stated and solved in Euclid II, 11. That means it has been of mathematical interest for over twenty centuries.

In the figure, B cuts segment AC into the golden cut. A demonstration on The Geometer's Sketchpad has been prepared. If you would like to see this demonstration after reading the directions which follow, click here. Once the Sketchpad is open, open a new sketch. (There will be a script for getting the golden cut for the segment you choose.) On the right hand side, draw two points by clicking the dot with the mouse. Use the finger to label these as points A and B. Be sure both points A and B are selected by putting the mouse pointer on them, one at a time, and holding down SHIFT. Then click on FAST on the script to find the golden cut for your segment.

Notice the ratio is 1.62 (the precision allowed by Sketchpad). If we label AB = x and BC =1, we have the following result:

, or
.

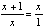
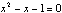
The positive solution to the quadratic is

= 1.61803, the value of Phi. The other solution, then, is
= - 0.61803 . This can be proved using the quadratic formula, since the quadratic will not factor over the integers.

and
,

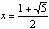
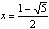
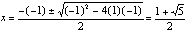
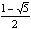
which equal 1.61803 and - 0.61803, respectively.

Back to Teresa Banker's Home Page