In an earlier investigation, the construction for the circle tangent to two given circles with a given point of tangency on one of those circles was developed. After reviewing the construction, the following question presented itself: What is the relationship between the distance between the centers of two given circles, one with a given point of tangency, and the sum of their radii to the circle tangent to both? In this essay, circle A contains the point of tangency C with radius AC; the second circle, called circle B, has a radius of BD; and, finally, blue circle T is the circle tangent to both circles A and B. In each figure, the red line passes through the center of circle A and the point of tangency C; the blue line contains the center of the blue tangent circle T; the other blue segments are necessary for the formation of the blue tangent circle. This investigation relies on the use of The Geometer's Sketchpad.
As you progress through the essay, you will find four cases investigated. Under each case there are three positions, where AB is the distance between centers and AC + BD is the sum of the radii: 1) AB > AC + BD ; 2) AB = AC + BD ; and, 3) AB < AC + BD.
Case 1: Circle A congruent to Circle B
Congruent circles have the same length radii, or, for our situation, AC = BD . Each of the positions investigated here are best achieved through animation of center point B along the unlabeled green segment (not segment AB). This will be reflected in the figures you see in case 1of the essay.
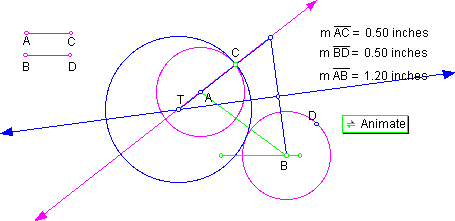
position 1: AB > AC + BD This construction is shown in Figure 1.

Blue circle T is externally tangent to both circles A and B, with circle A internally tangent to circleT while circle B is externally tangent to blue circle T.
position 2: AB = AC + BD as shown in Figure 2 .
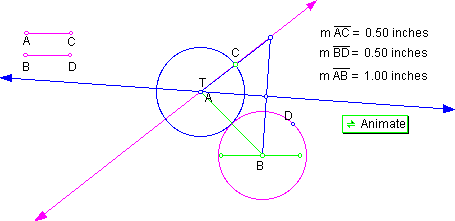
In this position where the distance between centers equals the sum of the radii, blue circle T and circle A are congruent and the same circle.
position 3: AB < AC + BD as shown in Figure 3.
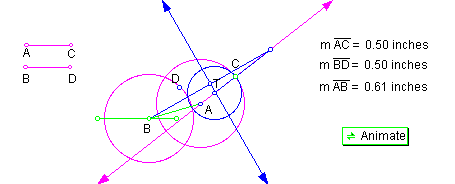
Here, blue circle T is internally tangent to circle A, while externally tangent to circle B.
Case 2: Center points A and B collinear with point of tangency C
For this case we have three considerations for each position: 1) AC > BD, 2) AC < BD, and
3) AC = BD. We will address each one.
position 1: AB > AC + BD as shown in Figures 4 and 5.
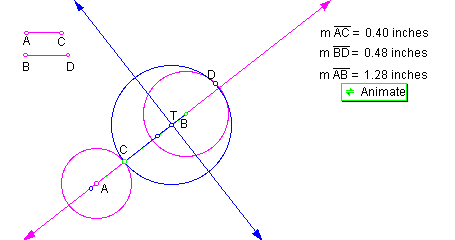
In Figure 4, blue circle T is externally tangent to both circles A and B, with circle B internal to circle T and circle A external and the smaller of the two circles. As it turns out, the size of the circles has no effect on the placement of the blue circle since the same configuration occurs. Also, the arrangement remains unchanged whether center point B is to the right or left of point C. Figure 5 shows circles A and B with equal radii.
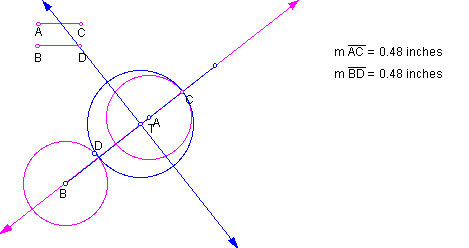
position 2: AB = AC + BD This construction is demonstrated in Figure 6.
For position 2 with the distance between centers equal the sum of the radii, the circles A and B, whichever is larger, will be congruent to blue circle T and, further, the same circle.
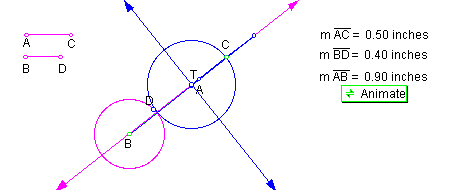
position 3: AB < AC + BD This construction is shown in Figure 7.
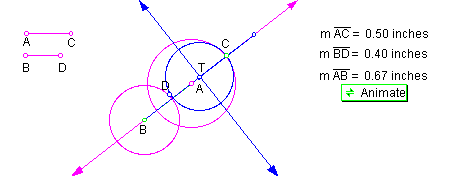
Regardless of which circle is larger, when the distance between centers is less than the sum of the radii, blue tangent circle T will be internally tangent to one circle, while externally tangent to the other.
Collinearity of points A, B, and C seems to create special properties which causes the same results in the location of the blue circle. Even the consideration of "B left of C" or "B right of C" does not change the results.
Case 3: Circle A is greater than Circle B, or AC > BD
For ease of demonstration, we chose to use animation of center point B along the unlabeled green segment (not AB).
position 1: AB > AC + BD , as shown in Figure 8, 9, and 10. There are three conditions to discuss, however, the configuration for circle T remains the same. Blue circle T is externally tangent to the other two circles when the distance between the centers is greater than the sum of the radii.
Condition 1: Angle APB is acute as shown in Figure 8.
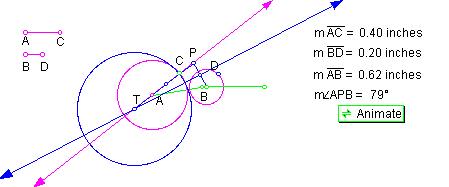
.
When angle APB is acute, circle A is always internal to blue circle T.
Condition 2: When angle APB is obtuse as shown in Figure 9.
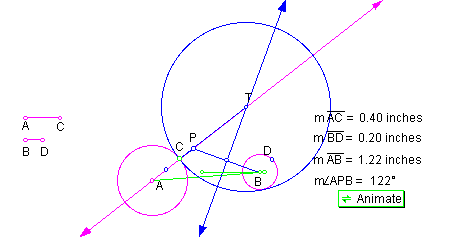
When angle APB is obtuse, blue circle T is external to both circles A and B, for the distance between centers greater than the sum of the radii.
Condition 3: When angle APB is a right angle as shown in Figure 10.
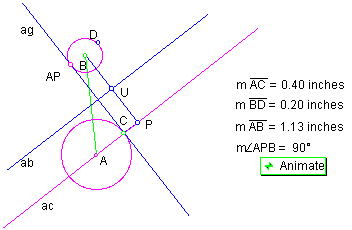
As angle APB approaches 90o, the radius blue circle T shown by arc ag approaches infinity, so ag looks like a straight line. Also, the line ac connecting A and C becomes parallel to the line ab which is the perpendicular bisector of BP. The center of circle T is infinitely far out in either direction on line ab.
position 2: AB = AC + BD, as shown in Figure 11.
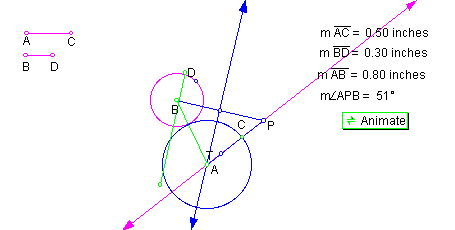
The result we see here is exactly the same as before: blue circle T and the larger circle, this time circle A, are congruent and the same circle when the distance and radii are equal.
position 3: AB < AC + BD , as shown in Figure 12.
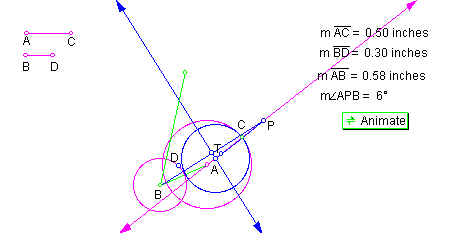
When the sum of the radii is greater than the distance between the two centers, blue circle T is internally tangent to the larger one and externally tangent to the smaller.
Case 4: Circle A is less than Circle B, or AC < BD
Again, for this case animation will be used to achieve the circle positions.
position 1: AB > AC +BD , as shown in Figure 13.
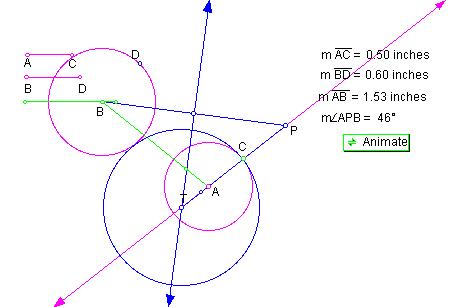
As we have seen before, distance between centers greater gives us blue circle T externally tangent to both circles with one internal and the other external.
position 2: AB = AC + BD, as shown in Figure 14.
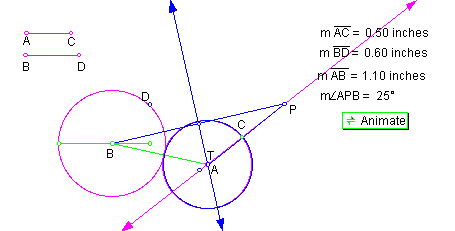
This figure confirms what we have seen before when center distance and radii are equal; blue circle T is congruent to one of our circles and the same circle.
position 3: AB < AC + BD , as shown in Figure 15.
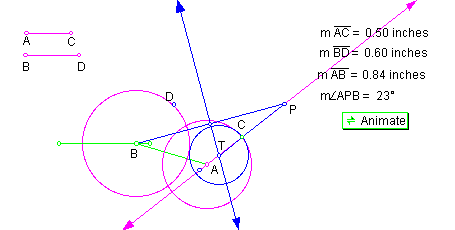
Once again, when the center distance is less than the sum of the radii, blue circle T is internally tangent to one of the given circles.
In doing this investigation, the focus became the distance between the centers of the two given circles compared with the sum of the lengths of the radii of those circles and the relationship to the circle tangent to both of the given circles. After pursuing four cases to related to the tangent circle configuration, the following can be said:
1) when the center distance is greater than the sum of the lengths of the radii, circle T is externally tangent to the given circles;
2) when the center distance is equal to the sum of the lengths of the radii, circle T is congruent to one of the given circles, and, in fact, the same circle;
and 3) when the center distance is less than the sum of the radii, circle T is internally tangent to one of the given circles and externally tangent to the other.
Back to Teresa Banker's Home Page