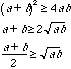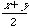 )
is greater than or equal to the geometric mean (
)
is greater than or equal to the geometric mean (
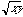 ).
We know that the following is true:
).
We know that the following is true:
Given two values X and Y, both being greater than or equal to
zero, we will prove that the arithmetic mean (
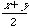 )
is greater than or equal to the geometric mean (
)
is greater than or equal to the geometric mean (
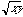 ).
We know that the following is true:
).
We know that the following is true:
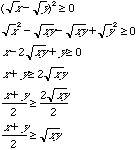
A comparison of arithmetic mean and geometric mean of a set a values for a and b can be easily visualized in a spreadsheet. The following is an example of a couple of rows from the attached Excel spreadsheet depicting values for a and b stored in columns A and B, respectively. The arithmetic mean is calculated in column C, with the geometric mean stored in column D. Example:
A B C D
1. 1 10 5.5 3.16227766
2. 5 99 52 22.2485955
3. 20 20 20 20
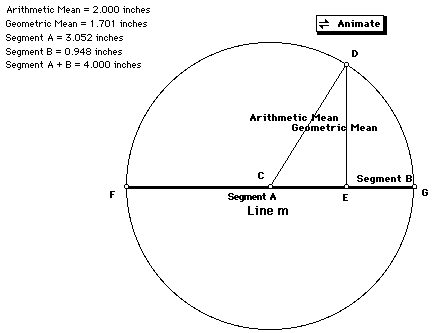
Through use of Geometry Sketchpad, two segments of length A and B
can be used to demonstrate that the arithmetic mean is always greater than the
geometric mean except when A and B are equal (both means are
equal under this condition) . The following sketch shows the two segments with
and a circle created with a diameter of the combined segments. The radius
CD represents the arithmetic mean
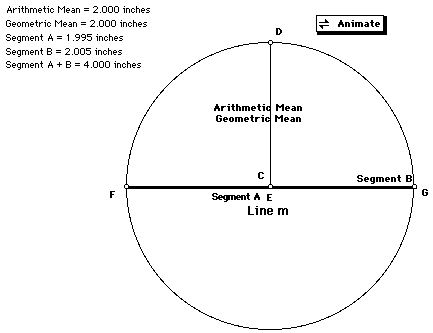
When segment B and segment A are equal in length, the following sketch shows
that arithmetic and geometric mean are equal.
By taking those same two segments, A and B, we can create a sqare with
sides of the combined lengths of A and B. The total area of the square will be
Once again, we have the left side of the equation representing the aritmetic
mean and the right side representing the geometric mean. Please launch the following sketch (by selecting) to see how the square is set up.
Back to
Mike Callinan's Home Page
Use of Geometry Sketchpad:
Circle: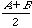 .
By dropping a perpendicular segment from the point D on the circle to
point E on the line m, we get a right trianlge with side
CE having a length of
.
By dropping a perpendicular segment from the point D on the circle to
point E on the line m, we get a right trianlge with side
CE having a length of
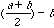 .
By knowing the length of the hypotenuse CD and one of the sides
CE, we can calculate the length of the other side DE as
follows:
.
By knowing the length of the hypotenuse CD and one of the sides
CE, we can calculate the length of the other side DE as
follows: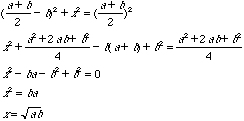
Rectangle Demonstration: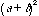 while the volume of the four rectangles with sides A and B are
while the volume of the four rectangles with sides A and B are
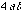 .
The former volume will always be greater than or at best, equal to the latter
as shown algebraically as follows:
.
The former volume will always be greater than or at best, equal to the latter
as shown algebraically as follows: