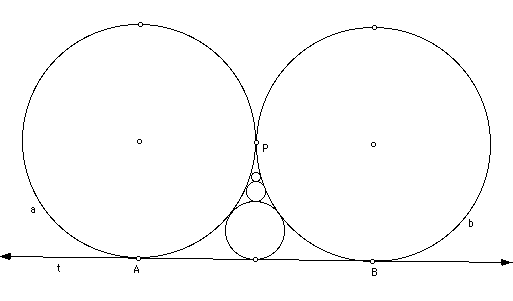
Shown below are two circles a and b of radius 1 touching at a point P. The line t is a common tangent and touches circle a at A and circle b at B. Circle c(1) has been constructed tangent to a, b, and t ; circle c(2) is tangent to a , b , and c(1); circle c(3) is tangent to a , b, and c(2). Suppose we continue to construct circles c(n) for n = 1, 2, 3, ... Some interesting conclusions can be made which relate to the radii and the diameters of these circles.

Our first task was to determine the radii of the circles c(n) .
To find the radius r1 of c(1), we drew PEX where X is the center of c(1).
Since PEX is a right triangle, then
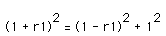
which led to r1= 1/4.
We then let Y be the center of c(2) and drew PEY. Then
PE = 1
EY = 1 + r2
PY = 1 - 2r1 - r2
Since PEY is also a right triangle,

and solving for r2 (with r1 = 1/4) led to r2 = 1/12.
Similarly, if we continue to construct circles c(3), c(4), and c(5), the following statements are true:

We then used MAPLE to determine
r3 = 1/24
r4= 1/40
r5 = 1/60
(NOTE: Once the radii of the circles were determined, we could then use GSP to do the initial construction in this essay.)
Thus far we had determined:
n radius diameter
1 1/4 1/2
2 1/12 1/6
3 1/24 1/12
4 1/40 1/20
5 1/60 1/30
We then began to look for a pattern. Letting r(n) and d(n) represent the radius and the diameter, respectively, of circle c(n), the observations we made were:
1) r(n) and d(n) are each reciprocals of even integers.
2) r(n) = 1/(4*t(n)) where t(n) is the nth triangular number.
3) d(n) = 1/[n(n + 1)].
4) r(n) = r(n-1)*[(n - 1)/(n +1)]
We then went to EXCEL to see if our observations could be verified.
Click here and select the file tancir1.xl to call up the spreadsheet.
Another observation concerned the sum of the diameters. It appears that if d(n) represents the diameter of circle c(n), then
d(1) + d(2) + d(3) + ... + d(n) = n/(n+1) Click here and select the file tancir2.xl to view the spreadsheet which indicates that the diameters are of the form 1/[n(n+1)]. We can also see that the sum of the diameters does approach a value of 1, as would be expected. Another observation that was observed was that the diameters are terms in the harmonic triangle. This triangle is displayed below.
1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9
1/6 1/12 1/20 1/30 1/42 1/56
1/12 1/30 1/60 1/105 1/168
1/20 1/60 1/140 1/280
1/30
In the harmonic triangle, the term in the ith row and the jth column is the difference of the terms in the (i-1) row, j column and the (i-1) row and (j+1) column. For example,
1/60 = 1/20 - 1/30 and 1/42 = 1/6 - 1/7.
REFERENCES
Cofman, Judita. What to Solve? New York: Oxford University Press. 1991. p. 97.
Fremont, Herbert. Teaching Secondary Mathematics through Applications, 2nd edition. Boston: Prindle, Weber & Schmidt. 1979. pp.276-282.