A Circle Tangent to a Given Line and a Given Circle

by Fhonda Danley & September Matteson

Problem: We are given an an arbitrary line and an arbitrary circle, construct a circle tangent to the given line and the given circle. What is the locus of the centers of all such circles?

First we must find one such circle. Let's use GSP to find this circle.

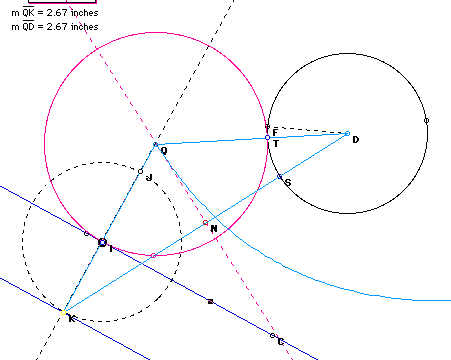
Construction: Construct an arbitrary line and an arbitrary circle. The line is dark blue and labled IC. The circle is black and labled D. We want to find a circle that is tangent to line IC and circle with center D. First find an arbitrary point on line IC. Let's call it point I. Make a perpendicular line through point I and perpendicular to IC. Now find radius of black circle, called FD. Copy radius onto point I and make a circle with center I. Circle with center I is congruent to circle with center D. Lable the intersection on the circle and the perpendicular line, point J and point K. Construct segment KD. Perpendiculary bisect KD with a dotted line. Lable the intersection of the perpendicular bisector and line KJ, point Q. Construct line QD. Now form circle with center Q and radius QI.

Z

Definition of Parabola: A parabola is the set of all points (x, y) that are equidistant from a fixed line (directrix) and a fixed point (focus) not on the line.

Using GSP, we can animate the pink circle and trace the center. We can see that the locus of the center of each circle forms a parabola. In the above picture, the parabola is light blue. The directrix is the dark blue line KZ. The focus of the parabola is point D. The distance from any point on the parabola to the directrix is the same as the distance from any point on the parabola to the focus. In this particular picture, Q is the point of the parabola, K is an arbitrary point on the dirextrix and D is the focus.

Proof: I want to prove that the locus of the centers of each circle forms a parabola. The definition of a parabola states that the distance from the directrix to any point on the parabola is the same as the distance from the same point on the parabola to the focus. Let D be the focus and KZ be the directrix. I constructed triangle KQD to be isosceles where

KQ = QD. We can also see that triangle QNK is congruent to triangle QND by side angle side. (I perpendicularly bisected KD. So KN is congruent to DN and angle QNK is congruent to QND and QN is congruent to itself). So triangle QNK is congruent to triangle QND. Therefore QK is congruent to QD. Thus the distance from the directrix to the center of the circle is the same as the distance from the center of the circle to the focus. The locus of the centers of the circles form a parabola.

What happens if the tangent surrounds the given circle?

Let's look at another picture.

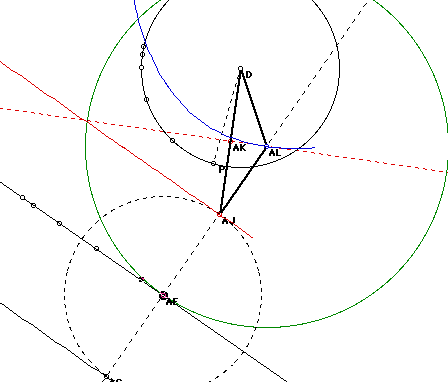
Construction: Construct an arbitrary line and an arbitrary circle. The line is black and labeled AF the circle is black with center D. Let AF be an arbitrary point on the line. Drop a dotted black perpendicular through AF and perpendicular to the line. Find raius of circle with center D and call it DP. Now form circle with center AF and radius of length DP. Label the intersections of the perpendicular line and the circle Af and AJ. Form a line from AJ to D. Perpendicularly bisect this line with a dotted red line. Label the intersection of the red dotted line and the black dotted perpendicular AL. Now form lines from AL to D and from AL to AJ. We have constructed an isosceles triangle where sides ALD and ALAJ are congruent. Now form a circe with center AL and radius ALAK.

Definition of a Parabola: A parabola is the set of all points (x,y) that are equidistant from a fixed line (directrix) and a fixed point (focus) not on the line.

conjecture: The foci of the green circles tangent to both the line and the circle forms a parabola. The parabola is blue. The focus is point D and the directrix is the solid red line.

proof: I want to prove that the locus of the centers of each circle froms a parabola. The difinition of parabola states that the distance from the directrix to any point on the parabola is the same as the distance from the same point on the parabola to the focus. Let D be the focus and the red line passing through the point AJ be the directrix. Let AL be an arbitrary center of a circle tangent to both a line and a circle. I want to show that AL AJ is the same length as AL D. I constructed triangle D AJ AL to be an isosceles triangle. We can prove that these two segments are congruent another way though. I perpendicularly bisected segment AJ d, so AJ AKis congruent to D AK and angle ALAKAJ is congruent to ALAKD. Since ALAK is congruent to itself, by SAS, triangles ALAKAJ and ALAKD are congruent. So ALAJ and ALD are congruent and have the same length. Since they have the same length, we can say that the foci of the circles are the same length from the directrix as they are from the fucus. Therefor the locus of the centers of the circles form a parabola.