1a. -What do the variables A, s, and i represent?

-Can you use this formula for concave and convex polygons?

-Can you use this formula for circles?

-How would you prove this formula?

-Use this formula to investigate patterns between the number

of nails and the area.

-How would you organize the information obtained using this

formula?

-Use this formula to find the area of Georgia and other states.

b.

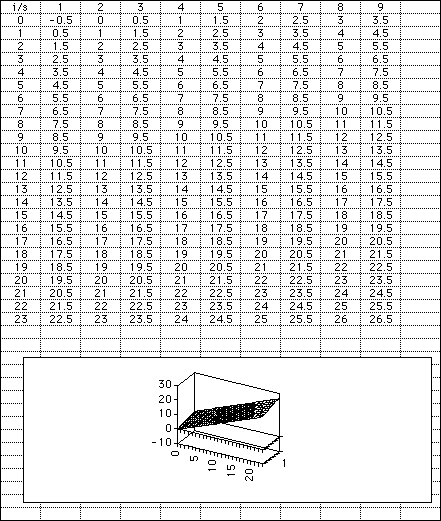
Spreadsheet

The students should create this spreadsheet in order to assist them in discovering patterns and to prove the formula. They can also use this to make a 3-dimensional graph to show that the areas lie in the same plane.

Algebra Expressor

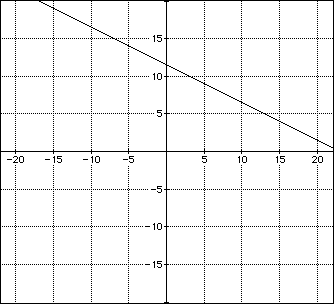
Students can use Algebra Expressor to find values of s and i which give a certain area. For example, students interested in finding values of s and i which give an area of 10.5 can graph the equation 10.5= (x+2y-2)/2, where x=s and y=i. This line represents all ordered pairs which give an area of 10.5.

GSP

Students can simulate a geoboard with unit 1 between each nail on GSP. They can create different polygons and use the tools available on GSP to find the areas of the polygons. They can check these areas using Pick's formula.

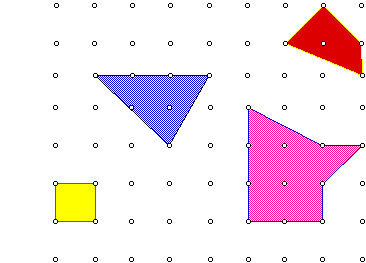
Yes, technology helps me to come up with different questions. Such questions might be:

1. Using the spreadsheet find the area of all polygons whose number of inside nails ranges from 1000 to 1100 and whose number of border nails ranges from 500 to 600.

2. Using Algebra Expressor find 10 examples of polygons which yield an area of 37.5.

3. Using GSP, illustrate 3 different polygons with area 37.5.

For example, when the students use the spreadsheet they can find the area of a polygon with a very large number of inside nails and border nails. With Algebra Expressor the students can identify exactly which ordered pairs will give a certain area. They will also realize that different ordered pairs will give the same area. Finally, with GSP the students can quickly visualize the polygons and determine their area.

Yes, the use of technology is imperative in answering these questions. You cannot answer the above questions without the use of technology.

2. Consider row 7. The first number in the row is 1. The next number in the row is "m" which is 7. The next number is P(7,2) + (m-1 + m-2)= 18. The next number is 18+(m-1 + 2(m-2))=34. The next number is 34 + (m-1 + 3(m-2))=55. Generalization for row seven: P(m,n)=P(m,n-1)+( (m-1) + (n-2)*(m-2)).!!!

Note, this formula P(m,n)=P(m,n-1)+( (m-1) + (n-2)*(m-2)) holds for all m and n.

3. Consider the sequence 1,3,4,7,18,29, . . .

Microsoft Excel is appropriate for this task.

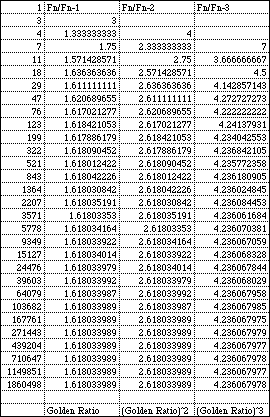
Using Microsoft Excel I have created the sequence up to the 30th term.

This sequence is related to the Fibonacci Sequence because each term is the sum of the two previous terms. However, this sequence begins with the numbers 1 and 3 whereas the Fibonacci Sequence begins with the numbers 1 and 1.

Furthermore, like the Fibonacci Sequence the ratio Fn/Fn-1 approaches the Golden Ratio. Likewise, the ratios Fn/Fn-2 and Fn/Fn-3 approach the (Golden Ratio)^2 and the (Golden Ratio)^3 respectively.

Have students investigate similar sequences such as

1,4,5,9,14, . . . and 2,5,7,12,19, . . .

How does it effect the ratio if the sequence begins with a number other than 1?

The only other software that I am familiar with is GSP and Algebra Expressor. I don't see how the use of either of these programs would aide in the investigation of Fibonacci-like sequences.

4. Yes there is a difference between contemporary general mathematics course for high school students and preservice/inservice teachers. Teachers should be inserviced as if they were the students themselves, but the interest level of teachers is much higher than that of most students. Teachers must experience learning through investigation in order to teach through investigation. However, we as teachers must not challenge general math students above their achievement level.

5. Computers support the idea that "The best way to learn is to do" because computers facilitate learning through exploration The computer allows students to quickly change values and see end results without any pencil-paper computations. Math students in general like computers. Computers hold the interest of most math students. Computers support the idea that "The worst way to teach is to talk" as well. Students will gain a better understanding of the concept learned and will retain this knowledge longer if they discover the information themselves rather than learning through the lecture method.

6. Yes, I am always learning things from my students. For example, a student told me that Pascal's triangle displays the powers of 11. Yes a teacher can learn from his or her students. Just as teachers prod students to persist in their learning, students constantly ask for answers to challenging questions.