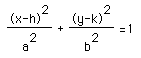
In a high school algebra text the definition for an ellipse states, "An ellipse is the locus of all points in a plane such that the sum of dipoints in the plane, called foci, is constant." Using the distance formula the Lust For Algebra leads to the standard form of the equation
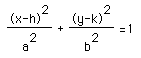

and the major axis is parallel to the x axis. This ellipse is easily graphed with software like Algebra Expresser because its capable of handling an equation that is not a function. To use graphing calculator technology for exploring the effects of h,k, a and b solve for y and enter the two resulting equations. For example,
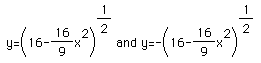
To see the ellipse develop from a geometric viewpoint click on the link to call up a Geometry Sketchpad demonstration based on the definition of the ellipse. Drag the foci to different positions and observe the relationship between a circle and an ellipse. Change the length of segment AB to see the different effects on the curve that result. See Sketchpad Ellipse. Interesting dynamics exist, although rather predictable and elementary.
When exploring parametric equations the ellipse appears quickly when equations x=a(cos(t)) and y =b(sin(t)) are graphed. The ellipse, center at the origin, has a major axis on the y axis when a<b. When a=b the ellipse is a circle with intercepts (0, b) , (0,-b) and (a,0), (-a,0). When a>b the ellipse is oriented with the major axis on the x axis. Continuing with the parametric explorations to more complicated equations of the type x=a(cos(t))+h(sin(t)) and y=b(sin(t))+h(cos(t)) the ellipse rotates and stretches as seen in the following graph of the equations x=2(cos(t))+sin(t) and y=3(sin(t))+cos(t).
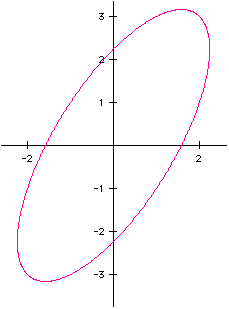
These parametric equations are strikingly like the equations generated by the rotation matrix. Suppose P(x,y) is a point on the graph of a conic section and P'(x',y') is its image after a counterclockwise rotation of theta. The values of x' and y' can be found by matrix multiplication. x'=xcos(t)-ysin(t) and y'=xsin(t) +ycos(t). What a neat connection!
The ellipse appears again and again when exploring tangent circles and loci involved with tracing various points. Click here to see the ellipse formed by tracing the centers of all circles tangent to two given circles at a given point. Click to see Sketchpad demo.
I expect to continue to encounter the ellipse as I continue to explore mathematics with its amazing connections. The ellipse continues to proliferate.