Sample of Student Summary

by Jon Whidby and Kelly Ferguson

A study of the following equations x=a sin(bt)
y= r cos(zt)

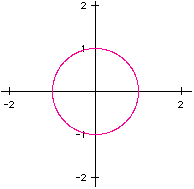
This is the graph of the original function for number 2. x=sin(t), y=cos(t) for the interval [0,2pi ]. This is the same as the graph of the unit circle, because the x and y values are the sin and cos of all angles on the interval of [0,2pi ].




The graphs of these functions, when coefficients, z and b, are added directly to t and the coefficients are equal, it simply continues around the circle the number of times that corresponds to the coefficient.

This is the graph of x= sin(.5t) and y= cos(.5t).






If b and z are different numbers, the b/z ratio determines the shape and density of line placement in the graph. If b/z ratio is low, lines follow the y-axis and become very dense as b/z becomes very small. If b/z ratio is large, lines follow the x-axis and become very dense as b/z becomes very large. a and r change the size of the rectangle containing the graph. Negatives change the initial direction the graphs follow but do not change the shape.

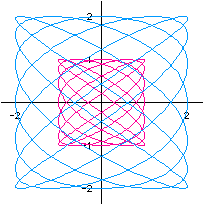
This is the graph of x= 2 sin(7t) and y=2 cos(5t) superimposed upon the graph of x=sin(7t) and y= cos(5t).



February 9, 1996

Jon Whidby and Kelly Ferguson