Most people are familiar with the number Pi, since it is one of the most ubiquitous irrational numbers known to man. But, there is another irrational number that has the same propensity for popping up and is not as well known as Pi. This wonderful number is Phi, and it has a tendency to turn up in a great number of places, a few of which will be discussed in this essay.
One way to find Phi is to consider the solutions to the equation
When solving this equation we find that the roots are
We consider the first root to be Phi. We can also express Phi by the following two series.
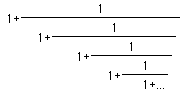 or Phi =
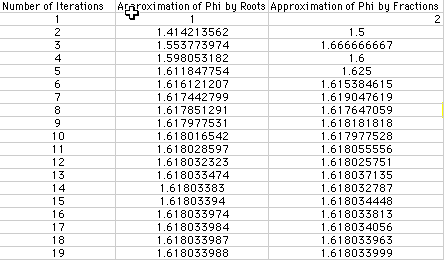
or Phi = We can use a spreadsheet to see that these two series do approximate the value of Phi.
Squaring both sides we have
But this leads to the equation
which in turn leads to
and this has Phi as one of its roots. Similarly, it can be
shown that the limit of the series with fractions is Phi as well.
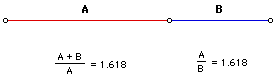
When finding the limit of the fractional series, we can take a
side trip and see that Phi is the only number that when one is
subtracted from it results in the reciprocal of the number.
I have creted a GSP script for dividing a segment (given its
endpoints) into the Golden ratio. If you would like to explore
this, click here.
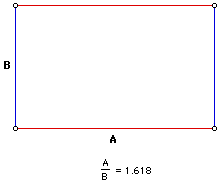
Another geometrical figure that is commonly associated with Phi
is the Golden Rectangle. This particular rectangle has sides A
and B that are in proportion to the Golden Ratio. It has been
said that the Golden Rectangle is the most pleasing rectangle
to the eye. If fact, it is said that any geometrical shape that
has the Golden Ratio in it is the most pleasing to look at of
those types of figures. Anyhow, here is a picture of the Golden
Rectangle.
Keep this rectangle in mind, I'll be coming back to it later.
But right now, I want to show where The Golden Ratio (Phi) pops
up in other geometrical figures.
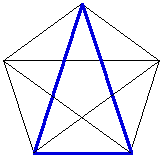
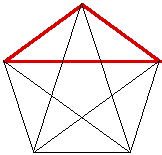
We can use the Golden Section to construct a regular pentagon.

If you would like to see a GSP script of this construction,
click here. If we connect the vertices
of the regular pentagon, we can get two different Golden Traingles.
The blue triangle has its sides in the golden ratio with its base,
and the red triangle has its base in the golden ratio with one
of the sides.
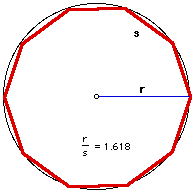
If we inscribe a regular decagon in a circle, the ratio of
a side of the decagon to the radius of the circle forms the golden
ratio.
If we divide a circle into two arcs in the proportion of the
Golden ratio, the central angle of the smaller arc marks off the
Golden Angle, is 137.5 degrees.

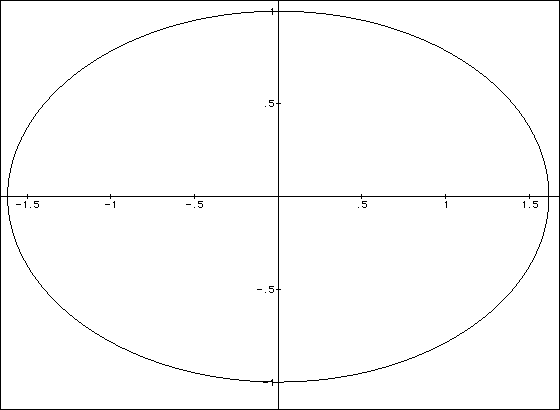
We can also form a Golden Ellipse. This ellipse has its two
axes in the Golden Ratio.
Let's turn back to one of the Golden Triangles for a moment.
If we take the isoceles triangle that has the two base angles
of 72 degrees and we bisect one of the base angles, we should
see that we get another Golden triangle that is similar to the
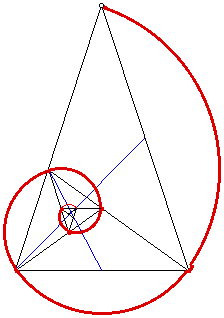
first (Figure 1). If we continue in this fashion we should get
a set of Whirling Triangles (Figure 2).


Out of these Whirling Triangles, we are able to draw a logarithmic
spiral that will converge at the intersection of the the two blue
lines in Figure 3.
We can do a similar thing with the Golden Rectangle. We can
make a set of Whirling Rectangles that produces a similar logarithmic
spiral. Again this spiral converges at the intersection of the
two blue lines, and these ratio of the lengths of these two lines
is in the Golden Ratio.
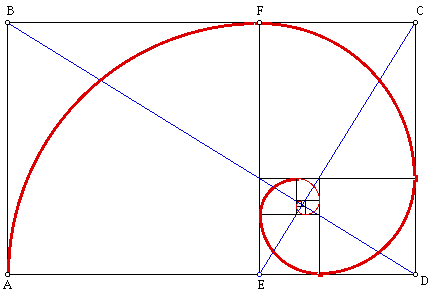
I will outline the proof that the ratio of the lengths of the
two diagonals is indeed the Golden ratio. Assume that rectangle
ABCD is a Golden Rectangle. Hence, AD/AB =AE/ED. But, FE = AE,
and so FE/ED= Phi. Hence, rectangle FCDE is a Golden Rectangle.
We have two similar rectangles and so since Phi = AD/EF then BD/CE
= Phi.
An interesting thing happens when we work with these whirling
rectangle. Suppose we take a rectangle of side 1 unit and a rectangle
of side 2 units and we put them side to side in the following
fashion and draw the appropriate segments to form a rectangle.
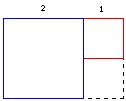
If we continue to create rectangles in this fashion we will
get a series of whirling rectangles like the one of above. The
following picture shows several such rectangles, and the lengths
of their sides.
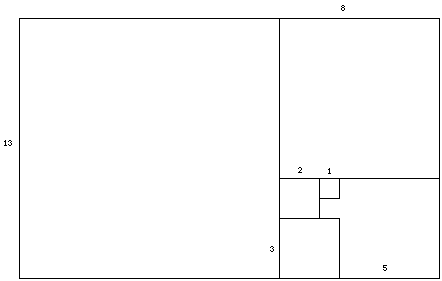
If we take ratios of the length we will see that the series
of whirling rectangles will begin to estimate the Golden Ratio.
Hence as we increase the number of squares we get a figure
that begins to look more and more like the Golden Rectangle. It
might also be noticed that there is something special about the
sides of the squares. If we list them we have, 1, 2, 3, 5, 8,
13, ... This of course is the famous Fibonacci sequence. As will
be shown in the rest of the essay, the Fibonacci sequence and
the golden ratio are intertwined with each other.
The proof is as follows.
Let F(n + 1) and F(n) be two consecutive Fibonnaci numbers and
suppose that p | F(n + 1) and p | F(n) . Since F(n + 1)= F(n)
+ F(n - 1) , then p | F(n) + F(n - 1) and so p | F(n - 1). We
also know that F(n) = F(n - 1) + F(n - 2), and by similar argument
we get that p | F(n - 2). If we continue in this manner, we'll
see that p divides every Fibonnaci number less than F(n + 1).
Hence p | F(2) and p | F(3). Since F(2) = 2 and F(3) = 3, then
p must equal 1. Therefore, 1 is the only number that will divide
both F(n + 1) and F(n) and we conclude that they are relatively
prime.
Another property that is verifiable by looking at the first forty
terms of the sequence, is that the Fibonnaci sequence is complete
with respect to the positive integers. This means that every positive
integer can be written as the sum of finite terms from the sequence
with no term being used more than once. For example, consider
the positive integer 257.
This representation is not unique since
The proof of this property is a straight forward inductive
proof and can be found in Maxfield and Maxfield (1972).
As was seen with the whirling rectangles, the ratio of consectutive
Fibonacci numbers begins to apporximate the Golden Ratio. A spreadsheet
can be used to see that this is more clearly the case. Values
of these ratios can be found in column B.
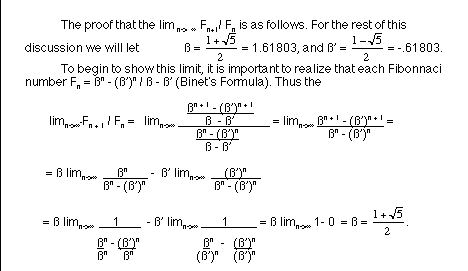
The second ratio that was considered was the ratio of every
other term, or F(n + 2 )/ F(n). The values for the computed ratios
for n = 1 to 40 are found in column C. As n increased, it could
be seen that there was again a limiting value of approximately
2.61803. This number also has significance with regard to the
golden ratio. We know that ß is one solution to the equation
x^2 = x + 1, and this equation tells us that ß^2 = ß
+ 1. When we do the arithmetic, we find that ß^2 = 2.61803.
The conclusion that we can then make from this is that the ratio
of F(n + 2 )/ F(n) is an estimate of ß^2, and this estimate
gets better as n gets larger.
Other ratios were of interest as well and the third ratio to be
considered was the ratio of every third term, or F(n + 3 )/ F(n).
The values for the computed ratios for n = 1 to 40 are found in
column D. As n increased, it could be seen that there was again
a limiting value of approximately 4.23607. This number also has
significance with regard to the golden ratio. If we consider the
system of equations
and make a substitution, we find that x^3 = 2x + 1. This means
that if ß was a solution to the equation x^2 = x + 1, then
we should be able to conclude that ß^3 = 2ß + 1. So
going through the arithmetic, we find that 2ß + 1= 2.61803.
So the next connection that we make is that the ratio of
F(n + 2) / F(n) has a limiting value of ß^3.
Finally the fourth ratio to be considered was the ratio of every
fourth term, or F(n + 4) / F(n). The values for the computed ratios
for n = 1 to 40 are found in column E of the spreadsheet. As n
increased, it could be seen that there was a limiting value of
approximately 6.8541, and again this number has connections with
the golden ratio. If we consider the system of equations
and make appropriate substitutions, we find that x^4 = 3x +
2. This means that if ß was a solution to the equation x^2
= x + 1, then we should be able to conclude that ß^4 = 3ß
+ 2. So going through the arithmetic, we find that 3ß +
2 = 6.8541. So the final connection we make is that the ratio
of
F(n + 4) / F(n) has a limiting value of ß^4.
So what hypotheses can we make from this sequence of discussions?
First, if we were to continue to solve equations, we could find
a general formula for any power of x. This being
Using this equation, we can compute any power of ß simply
substituting ß in for x. The proofs of these facts should
follow from a simple inductive process. The last hypothesis that
we make is that, for any integer k> 1,
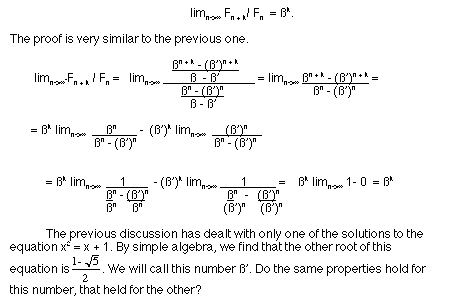
The first question to be answered would be, "Is ß'
the limiting value of some ratio of the Fibonnaci numbers as they
go towards infinity? The answer is yes. If we consider the following
ratio
F(n)/ F(n + 1) and consider the limit of this as n goes to infinity,
we do get the value of ß' = -.61803. The value of the first
thirty-nine ratios can be found in column F of the spreadsheet.
We can also go through a similar process with the ratios of F(n)/F(n
+ 2 ), F(n)/F(n + 3 ), and F(n)/F(n +4), and see that the same
properties hold for ß' that held for ß. The values
for these ratios are in the spreadsheet columns G, H, and I respectively.
The spreadsheet was used in another way to help analyze the Fibonnaci
sequence. It allowed us to easily change the first two numbers
of the sequence and therefore allowing us to change the entire
sequence. Many different values were tried including positive
and negative integers and decimals of varying length. The very
interesting event that happened was that the ratios always estimated
their appropriate power of ß of ß'.
Also, the spreadsheet enabled us to look at the formula F(n -
1) * F(n + 1) - F(n)^2 for n a positive integer less than or equal
to 40. The resulting values are in the spreadsheet column J. The
values are somewhat interesting. When n is even we get 1, and
when n is odd we get -1. Hence, we hypothesize that
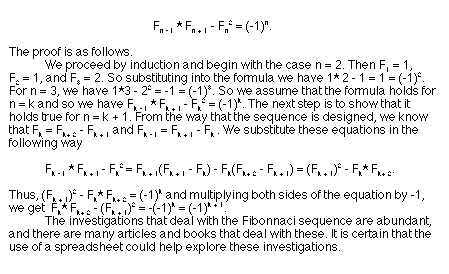 \
\
Certainly there are many more areas to explore. For example,
can the ratios in columns B through E be represented geometrically?
What other ratios can I form using the Fibonacci sequence and
still have the limit of the ratios converge to a particular number?
What relationship would these numbers have to the Golden Ratio?
I'll leave these questions for other people to answer, for right
now, I think that it is time I moved on to something else.
Maxfield, J. E. & Maxfield, M. W. (1972). Discovering number
theory. W. B. Saunders Co: Philadelphia, PA
Gardner, M. (1961). The second scientific American book of mathematical
puzzles and diversions. Simon and Schuster: New York, NY.