Using GSP to Teach Lines

by Mark Freitag

One of the topics that most students encounter at one point or another is the concept of a line. Topics that might be included in such a discussion are slope, linear equations, x and y-intercepts, perpendicular lines, and parallel lines. One approach to teaching these concepts is to have the students graph the lines using pencil and paper and then have them try to notice patterns that occur. Unfortunately, until students become efficient at graphing lines this approach can be time consuming and ineffective. This situation can be remedied by using the program Geometer's Sketch Pad. Certainly, the line is one of the most basic geometric figures, and GSP provides a dynamic environment for studying them. This essay is a demonstration of how GSP can be used to teach the lines in a manner that allows the students to discover the nature of the concepts. I hope to provide the reader with example GSP constructions as well as several questions that might be posed to the students to guide them in their exploration. While I have presented the demonstrations in a particular order, the teacher should feel free to rearrange the screen in any order appropriate.


To begin the exploration, the teacher might create the following screen.

To make this screen enter GSP, turn on the Axes but not the grid. If you leave the grid on, it could make the motion of the line "jerky." Next, simply construct a line between two points A and B. This is the basic model for the exploration. GSP will allow the explorer to dynamically change the line in two ways. By clicking on the line, the explorer can move the line with out changing the slope. By clicking on one of the points, A or B, the line will rotate about the other point, thus changing the slope. If you have GSP on your computer and would like to explore the basic screen click here.

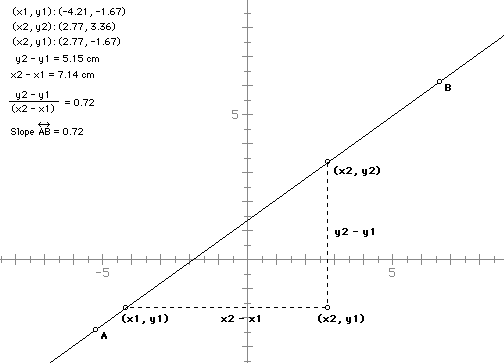
Certainly this is not very exciting, but by adding a few more things, it can be made into a wonderful place for exploration. One of the first things that can be done is to give the coordinates of the points A and B. As the line is moved it should be noticed that the coordinates of the points change. Once we have the coordinates of these two points and the corresponding coordinate system, we can begin to explore one the the fundamental concepts of the line, slope.

A basic way to define slope is the ratio of the rise over the run. In other words, if given two points, (x1, y1) and (x2, y2), the slope of the line is defined as (y2 - y1)/(x2 - x1). By adding the following features to the basic screen, the GSP line environment is ready for exploration.

The following guide/questions might help the students get more out of the exploration.

EXPLORATIONS

1) Move the point B.

Describe how the coordinates of the various points (x1, y1), (x2, y2) and (x2, y1) change.

Describe how the difference of the x coordinates change (x2 - x1).

Describe how the difference of the y coordinates change (y2 - y1).

Is there a connection between the ratio of the differences and the slope of the line AB? Can you make a generalization from this?

As the line approaches horizontal, what happens to x2 - x1? y2 - y1? the slope of AB? When the line is horizontal can you explain why the slope is what it is?

As the line approaches vertical, what happens to x2 - x1? y2 - y1? the slope of AB? When the line is vertical can you explain why the slope is what it is?



2) Move the point A to the lower right hand corner of the screen (4th quadrant), and move the point B to the upper left hand corner of the screen (2nd quadrant).

Did the slope change? How? Can you explain why?

Can you describe when the slope will be positive and when it will be negative?

How does this relate to the points (x1, y1), (x2, y2) and (x2, y1)?



3) Summarize what have you learned about the slope of a line.


These are just a few questions to get started, and the teacher should feel free to add others. By moving the various points around, the students should get a feel for the concept of slope. At the bare minimum, they have seen many different lines in a short period of time, and they did not even have to graph any of them. If you have GSP and would like to explore this set up click here


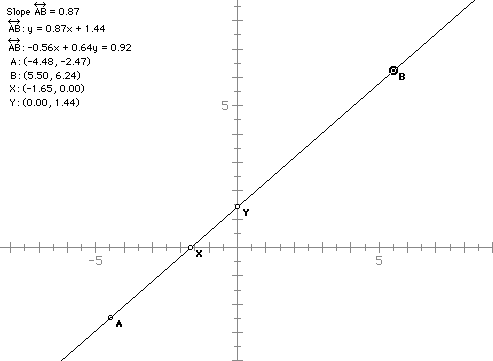
Once the concept of slope has been taught, the next demonstration might include equations of a lines and the intercepts of the lines. GSP can be used to explore these ideas, although the teacher should probably include an algebraic derivation of the formulas as well. This depends on the situation. Again, I have provided a sample screen as well as some example questions to guide the exploration.

In this picture, X is the x-intercept and Y is the y-intercept. I have provided the equation of the line AB in both Standard and slope-intercept form.

EXPLORATIONS

1) Move the point B.

How does the coordinates of the x-intercept change? the y-intercept?

When are X and Y the same?

How do the equations of the lines change? Can you generalize this?

Do you see a connection between the two equations of the line AB?



2) Move the point A to the lower right-hand corner and the point B to the upper left-hand corner. Answer the questions in the first exploration.



3) Move the point A to the origin (the point (0, 0)). Drag the point B.

As you drag B towards the x-axis, what do you notice about the slope of AB and the equations of the line AB?

When the line is horizontal (What is the y-coordinate of B?), what happens to the intercepts, the slope of AB, and the equations of the line? Can you explain each of these?

As you drag B towards the y-axis, what do you notice about the slope of AB and the equations of the line AB?

When the line is vertical (What is the x-coordinate of B?), what happens to the intercepts, the slope of AB, and the equations of the line? Can you explain each of these?


4) Summarize what you have learned in this exploration.


If you have GSP and would like to explore this set-up, click here.


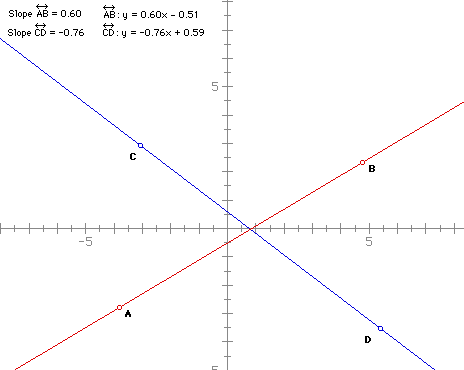
From these explorations, it is hoped that the students will have learned many of the topics concerning lines. But we are not done. GSP can be used for at least one more demonstration about lines. It can be used to show the relationships between perpendicular and parallel lines. This exploration might be started using the following screen with two lines.

EXPLORATIONS

1) Move the lines around by dragging various points or the lines themselves.

Can you make any observations about the slopes of the two lines?

What happens when the lines are perpendicular?

What happens when the lines are parallel?

Can you make any conjectures?


If you would like to explore this screen, click here.

It is hoped that the students will make some sort of conjectures about the nature of perpendicular lines. To test these conjectures, the following screen might be used.

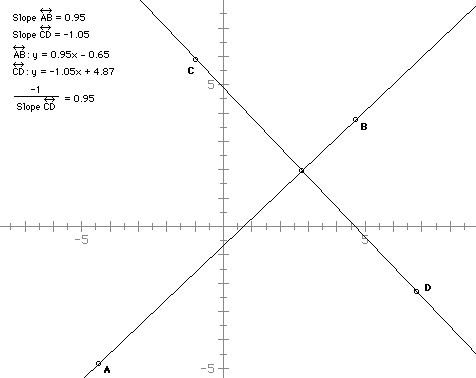
EXPLORATIONS
1) Drag the point B.

What do you notice about the equations of the two lines?

What do you notice about the slope of the two lines? (Use all the information on the screen if necessary)

Since the two lines are perpendicular, what conjectures can you make about the lines?


If you would like to explore this screen, click here.

It is hoped that the students will make some sort of conjectures about the nature of parallel lines. To test these conjectures, the following screen might be used.

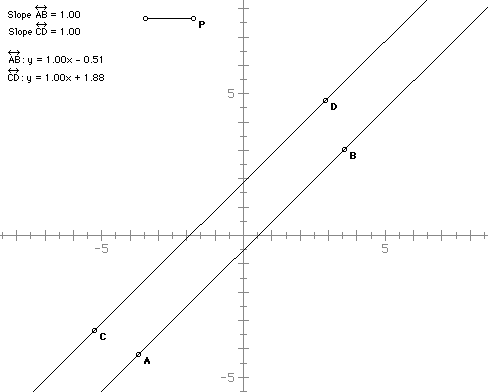
In this particular case the lines are made so that the distance between them remains the same as the point B is dragged. To change the distance between them drag the point P on the line segment at the top.

EXPLORATIONS
1) Drag the point B

What do you notice about the slopes of the two lines?

What do you notice about the equations of the lines?

Is there a connection between the two y-intecepts in the picture? the two x-intercepts?

What conjectures can you make about parallel lines?


If you would like to explore this situation and you have GSP, click here.

The concepts of lines can be difficult for students to understand, and perhaps one way of clearing up misconceptions is for students to have as much experience with lines as possible. In the past, teachers and students have been limited in the number of lines they have been able to investigate because of time and "technology restraints" But with GSP demonstrations, the teacher and students will be able to consider and investigate many more lines in a short amount of time. The program allows the investigator to move the lines with out having to draw a new graph. Certainly, an algebraic approach should also be used, but I really believe that the dynamical nature of the program can help the student to develop a solid understanding of concepts such as slope and intercept.


Return to Mark Freitag's Homepage