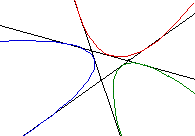

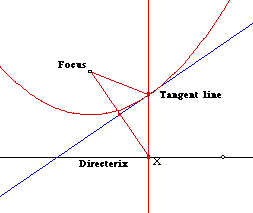
Notice that we have located a point equidistant from the focus and the
directerix as the vertex of an isosceles triangle, which was created using
the intersection of a perpendicular to the directerix at point X and the
perpendicular bisector of the segment from X to the focus. Once we have
our parabola, we can draw in an isosceles triangle and its perpendicular
bisector, which is the line tangent to the parabola through the triangle's
vertex.
Through investigation and experimentation, we can find three particular
points on the parabola which give us some insight into finding a parabola
tangent to three specific lines:
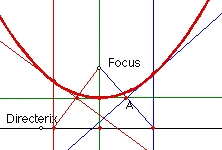
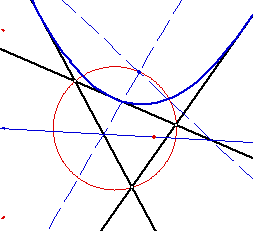
Because of their construction, the tangent line and the line connecting
the focus and the directerix are perpendicular in all three constructions,
for example, the blue lines are perpendicular through point A. Also, because
of the particular tangent lines chosen, two tangent lines intersect at that
perpendicular intersection; the blue and the green tangent lines intersect
at point A.
It occurs to us, then, to look for a focus by creating perpendiculars to
our original lines through the vertices of the triangle. If this works,
then the following three points will be foci for three of the parabolas
we are looking for:
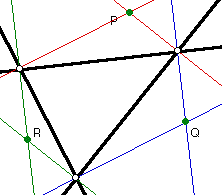
(Notice that these are not the ONLY points where these six lines intersect;
there are six other points of intersection, but the points P, Q, and R are
the only ones that we are interested in at the moment.)
Thinking back to our sketch of the parabola and three of its tangent lines,
we notice that the vertex of the parabola lies on the side of the triangle
not used in creating that parabola's focus. From this, we know that the
directerix is parallel to that side, and its distance from the side is equal
to the distance from the focus to the triangle's side.
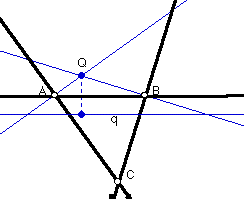
For example, given triangle ABC, below, and having found Q, our supposed
focus, we find our directerix, q, by reflecting Q about side AB and constructing
a q parallel to AB through our the reflection.
When we do this for all three sides, we get the parabolas we are looking
for!
Click here for a dynamic look at these
parabola. Drag the vertices of the triangle around, and be sure to examine
what happens when the triangle is a right triangle and when it is an obtuse
triangle.
In an obtuse triangle, all three of these special parabolas migrate to one
side of the triangle, leaving no parabolas on tangent to the other two sides!
It seems, then, that there must be more than three parabolas that fit our
original conditions.
In fact, any conic is uniquely defined by exactly five tangents. Since we
are interested only in parabolas at the moment, one of these tangent lines
is at infinity. We have only three other tangent lines specified, so it
is feasible that there are an infinite number of parabola that fit our conditions!!
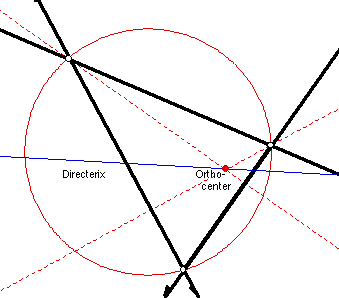
Notice that no matter what, the three directerices are concurrent. Through
exploration, we determine that this point of concurrency is the orthocenter
of the original triangle. Also, exploration suggests that the three foci
are incident with the circumcircle of the triangle. We can illustrate this
nicely on Geometer's Sketchpad (click here),
but for the moment we will not attempt a proof. We will first use these
discoveries to become more familiar with this special set of parabolas.
Through further exploration, we discover that for any point on the circumcircle,
we can find a line such that the point and the line are the focus and directerix,
respectively, of a parabola tangent to the extended triangle. We also discover
that all of the directerices are incident with the orthocenter of the triangle.
This inspires a wide array of questions:
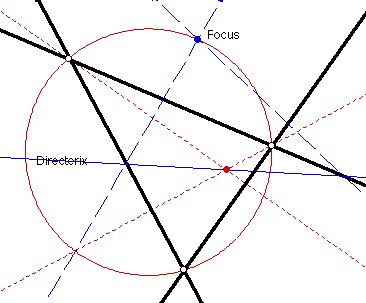
If we think about creating a parabola by folding paper in order to "connect"
the focus with a point on the directerix, we see that the folds created
are the lines tangent to the parabola. Or we can think of these folds as
lines of reflection. Well, we have three such lines, and when we reflect
our directerix about any one of these lines, we know that our focus will
lie on that reflection! When we reflect about two of the lines, we have
our focus: the intersection of the reflected lines.
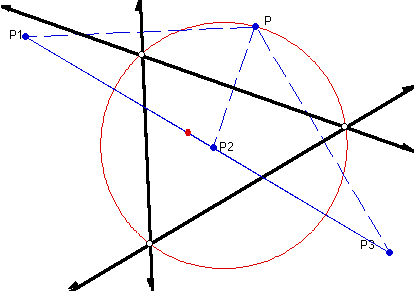
So, for every directerix, we can construct our focus. Also, for any focus,
we can construct our directerix, and, as illustrated in this animated sketch
(click here), the relationship is one-to-one.
Given any focus on the circumcircle, it seems to be the case that reflection
about any of the three lines, together with the orthocenter, determines
the directerix. This implies that, given any point on the circumcircle of
a triangle, the reflections of that point through each of the three extended
sides are collinear! Since only a point on the circumcircle seems
to work as a focus for a parabola that fits our conditions, it may be the
case that a point not on the circumcircle will not yield three
collinear points when reflected about the lines of the triangle.
We can get a handle on whether or not this idea has merit with a GSP sketch.
Click here.
So, it seems that we have boiled much of this problem down to proving a
collinearity result.
As a matter of fact, through similar triangles, we can reduce this issue
even more:
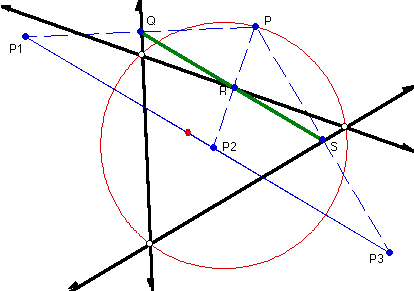
Notice that triangle PP1P2 is similar to triangle PQR. This is because
Q is the midpoint of PP1, since it lies on the mirror which created P1.
Also, R is the midpoint of PP2 for the same reason. By the same reasoning,
triangles PP2P3 and PRS are similar. So, proving that Q, R, and S are collinear
implies that P1, P2, and P3 are collinear.
Notice that the segments PQ, PR, and PS are simply the perpendiculars to
the three extended sides of the triangle, with the intersections being Q,
R, and S. So, we are simply dealing with the feet created by dropping perpendiculars
from point P.
Any point not on the circumcircle, when we drop perpendiculars to the triangle's
extended sides, will yield the vertices of triangle; on the other hand,
any point on the circumcircle will yield collinear points, perhaps simply
a degenerate triangle. Here is where I am currently stuck; it seems that
this collinearity result could be found in a consequence of Desargue's collinearity
results or Pappus' theorem, but I have not made a connection. It can be
proven using coordinate geometry, but it is so long, tedious, and unilluminating
that it is hardly worth the effort to write it down. (That is simply my
opinion; my geometry professor would vehemently disagree, and the fact that
the proof was so unilluminating probably has more to do with my discomfort
with the intricacies of linear algebra than anything else. )
I seem to have neglected the orthocenter; I think this is because the only
connection I have made so far is that any point on the circumcircle, when
reflected about all three lines of the triangle, produces three collinear
points, and the line incident with those three points is also incident with
the orthocenter of the triangle. However, I think that proving that the
perpendicular intersections Q, R, and S are collinear will reveal a great
deal about the orthocenter.
I invite anyone in future 668, 669, or 670 classes to pick this up where
I leave off. I have altered the original question; it now seems to be about
collinearity. However, when this collinearity result is proved, the original
issue seems quite understandable through the power of reflections and the
definition of a parabola.