A Short Interlude with Polynomial Tables

by
Paul Godfrey

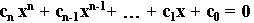
In mathematics we often times find solutions to problems by seeing patterns. In many practical branches of mathematics, such as statistics and chaos theory, patterns become critical. In the following exploration of the polynomial table, we intend to look for patterns. I report here some of the patterns I found. There are many others. After looking at the ones presented here, you are invited to see what other patterns you can find.

Computers make explorations quicker and more fun (you don't have to worry about your arithmetic). The figures presented are from the trademarked "Microsoft Excel" spreadsheet. Only the first ten rows of the table are presented. However, the table numbers are links to "Excel" files that contain more rows, along with the formulas for expanding the rows to the limits of the spreadsheet. Merely click on the link to get a copy of the file.next
Polynomials are algebraic expressions. A single variable polynomial consists of a variable, say x, which is expressed as an equality as follows:

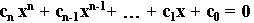
Here, the ci's are real numbers and often called coefficients, although sometimes referred to as constants. A special class of these polynomials are those that can be expressed as

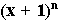
For example, if n were 2, we could write the polynomial expressed by

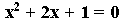
For n = 3, we would write

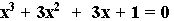
In general, we can construct a table, using only a spreadsheet program, which will give us the coefficients of this polynomial for any value of n. The following is such a table.next

Table 1
We notice that there are some patterns in this table. First, we see that the first column is all 1's. That is not surprising. The second column, though, is in counting number order. That is, 1, 2, 3, 4, 5, etc. How about the next column? The difference from 1 to 3 is two, 3 to 6 is three, 6 to 10 is four . . . well, it looks like we have a pattern here doesn't it? The next column has a pattern, too. Do you see it? The numbers 3, 6, 10, 15, 21, 28, 36 are the differences between the shown values, and what is the pattern of this? Look at the preceeding column (ignoring the 1, that is)! Does the next column follow the same pattern? We have 1 to 5 differing by four, 5 to 15 by ten, and so on so that the differences are 4, 10, 20, ..., just like the numbers in the preceeding column, again, if we ignore the 1. We see the same for the next, and the next, and so on. Interesting, you might say, but so what?next
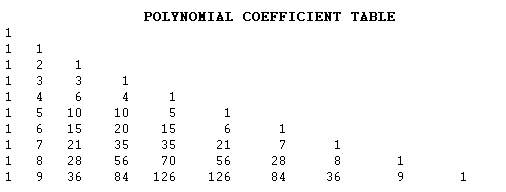
Another pattern we can see is when we add up the rows. The order of the row somes is the same as the powers of 2!


Table 2
next
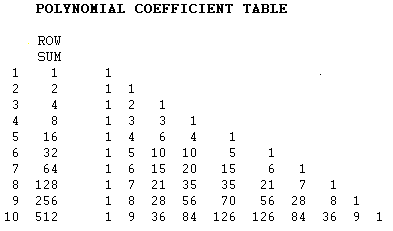
Are there other patterns? Of course. Just look at the left to right diagonals. The first one is all ones, just like the first column. The second left-right diagonal is like the second column, and so on.


Table 3
next
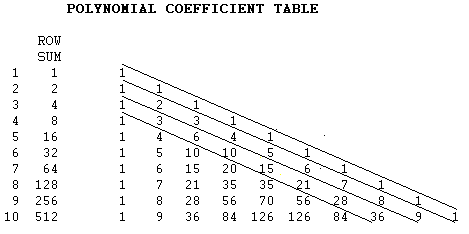
How about the Fibonacci numbers; they seem to be everywhere, how about here? Well, if we add up the right to left diagonals, that's just what we get as seen in this next picture.


Table 4
next
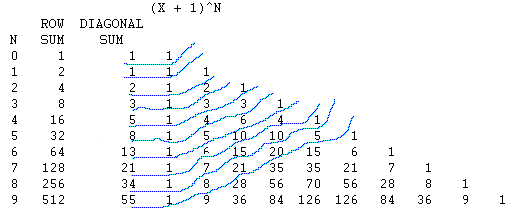
Notice in the previous figure I substituted the equation 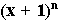, written as (X + 1)^N, rather than Coefficient Table. This next figure inserts a column that represents the power N. I've increased the size of the appropriate rows in the next table to reflect the next pattern. Can you see what it is?


Table 5
When N is a prime number, all the numbers on it's row between the ones are divisible by N.next

There are more patterns still to be discerned in the table presented here. I hope this presentment encourages you to seek them.

Return to Home Page