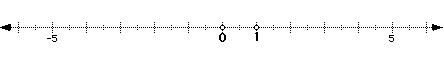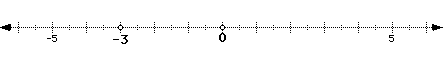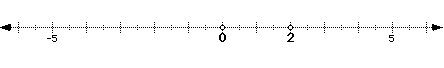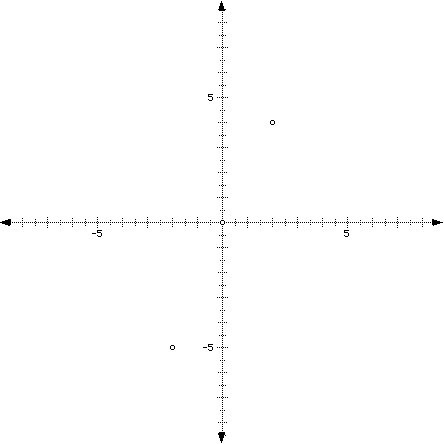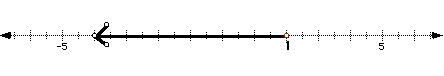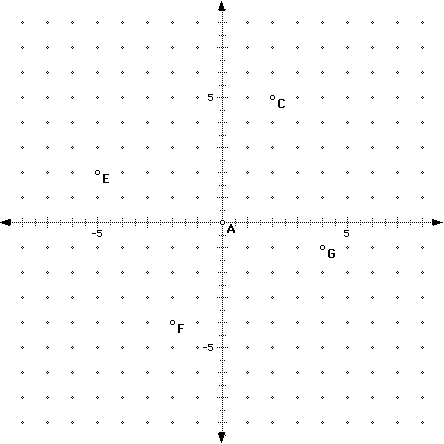Teaching Unit

---

Drew Cronic and Chris Hood

---

Equations and the Number Line
Inequalities and the Number Line
Ordered Pairs
The Coordinate System
Equations with Two Variables
Graphing Equations
Slope
Intercepts

Unit Goal: The students should be able to graph solutions to equations and inequalities and graph equations using slope and x&y intercepts.

---

Goal: The students should be able to graph solutions of equations on a number line.
Objectives:
1. The students should be able to solve one variable equations and graph the solution.
2. The students should understand the possibilities for representing data on a number line.

Lecture: I would begin the lesson having a number line created in G.S.P.. I will remind the students that this demonstration is a number line.


What do the arrows mean ?
I will tell the students that the numbers represent a coordinate of a point and its direction from zero. The students have learned that when they solved equations they found a solution, so now I will teach them to graph the coordinates on a number line.

Examples:
1. y+4=5 check: y+4=5 2. 9x+2=5 check: 9x+2+5
-4 -4 1+4=5 -2 -2 9(1/3)+2=5
y=1 5=5 9x=3 3+2=5
9 9 5=5
x=1/3
A good idea would be to have the students come up and point with the mouse where the points should go.
1)

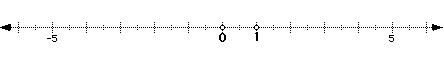
2)

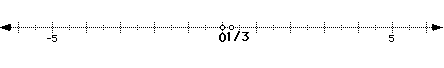
Example:
3. 2a+4a-1=19 check: 2a+4a-1=-19
6a-1=-19 2(-3)+4(-3)-1=-19
+1 +1 -6-12-1=-19
6a=-18 -19=-19
6 6
a= -3
3)

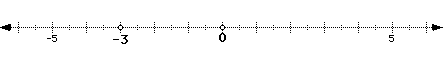
Now, I will ask the students to write an equation for the following graph and explain why you know your equation is right.

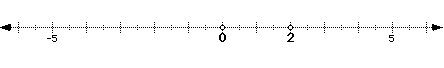
4 Use a number line to express the low temperature last night was 30 degrees. Tell the students that for this problem we are expressing data on a number line.



Ask the students does it matter how we mark our number line. Tell them that the increments of our number line must be equal and that the numbers should increase from left to right.
A possible misconception is the graphing of decimals and fractions.
Homework will be given as classwork. Problems will include real world problems and the same problems used above in the examples.

First, I will ask some of the students to put particular problems on the board from the homework and while they are doing this I will go around and check the homework.

Goal: The students should be able to graph the solutions of inequalities on a number line.
Objectives:
1. The students should recognize the difference in the open and closed point or another alternative is the use of parentheses as a way of expressing the open dot.
2. The students should recognize where to bold the line in the appropriate direction.
3. The students should appreciate the possibilities of using a graph to represent data.

First, I will begin by reviewing the different symbols used for inequalities. I will start the class with an example representing the speed limit on interstate 85 in Georgia. I will prompt the students to produce an inequality that represents the speed limit on this interstate. I will let s stand for speed.
So s<=70.
( Because G.S.P does not allow closed dots I would represent inclusive with black point and noninclusive with red point)
The graph:

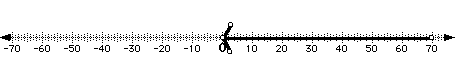
Then we would do an inequality that represents all illegal speeds. s>70

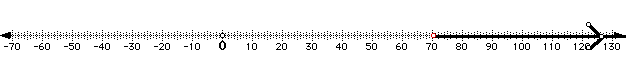
Notice that 70 is not included in the solution.
Do some more examples of graphing inequalities with open and closed dots.
Another example: Graph x>=0 or x<2

Notice that 0 is included and 2 is not included.
Possible Misconceptions:
1. Forgetting to change the direction of the inequality symbol when dividing and multiplying by a negative number.
2. Understanding of the open and closed dots..

Remaining classwork and homework: I will choose problems from the book for them to do. I will make sure that some challenging problems are given.

Same routine for homework is done.

Goal: The students should be able to graph points in the Cartesian Plane.
Objectives:
The students should understand:
1. how to recognize an ordered pair (x,y) with being the horizontal shift and y being the vertical shift.
2. to always move horizontally first then vertically.
3. to label the axes and origin.
4. the location of all four quadrants and their appropriate signs.

First, I will introduce the students to the Cartesian Plane and explain who it was named after ( Rene' Descartes ). I will also explain that the Cartesian Plane is just one horizontal number line and one vertical number line that intersect at 0. I will explain that this point is called the origin and the horizontal number line is the x-axis and the vertical the y-axis.
I will now begin to graph points in the Cartesian Plane to explain how to graph ordered pairs (x,y).

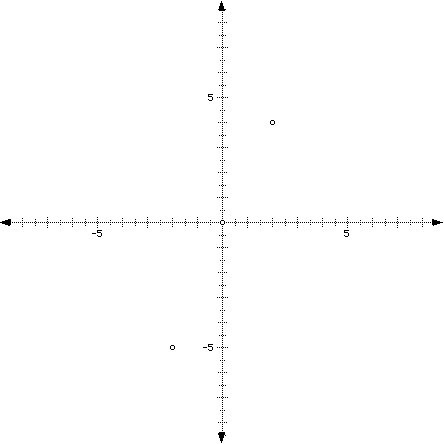
I would also mark some points on the Cartesian Plane and ask the students to give me the ordered pair. A worthwhile task that could be implemented for graphing ordered pairs is the game of battleship. This would be enjoyable for the students and they would be getting familiar with graphing ordered pairs in the Cartesian Plane. No homework, but a quiz will be given on the next day.

Solve and graph:
1.2y+4=16
2. Write an equation that would provide the following solution:

Graph:
3. y>3
4. x<=-5
5. Write an inequality that describes:

From the following set of axes, write the ordered pair that corresponds to each point and tell what quadrant it is in.


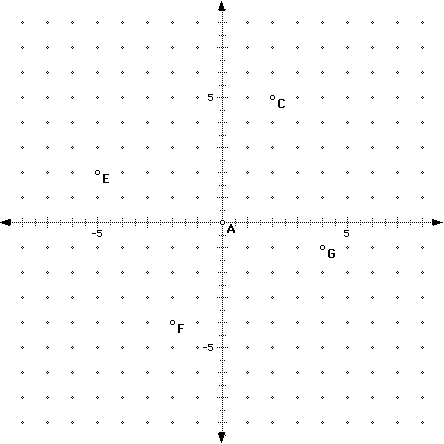
Graph the following points ( remember to label your axes and points ).
A( -4,3) B(2,-1) C(0,0)D(-6,-2)

After quiz is finished a review will be given.

Goal: Our goal is for the students to know how to solve equations with two variables, and how to graph these equations using coordinates.

Objectives for 8.5:

1) We want our students to recognize that putting values in for x is the easiest way to determine y-values.

2) We want our students to understand that at least two points must be determined before a line can be graphed.

3) We want our students to understand that the final solution to an equation is not one number but is expressed as an ordered pair.

4) We want them to understand that there are infinitely many solutions to an equation with two variables.

5) We want to introduce them to the technique of using tables to organize their thinking and solutions.

Objectives for 8.6:

1) We want to review graphing ordered pairs.

2) We want our students to understand that graphing is a step by step process.

3) We want the students to recognize other solutions to the equations from the graphs.

4) We want to introduce the term " linear equation", and we want them to be able to recognize what a linear equation looks like.

Lesson Plans:

Day 5
- We will begin discussing solutions to equations.
- Introduce tables.
- We will let the students create a table from an example equation. (An interesting and real world example that will call for them to create their own equation). We will provide coaching during this time. In addition, we may let some students write their tables on the board.
Real World Example:
Forests serve as the only source of timber. Sometimes the production of timber conflicts with the need to conserve the environment and wildlife. In an effort to conserve both the forests and the wildlife, foresters replace the tress that have been cut down. About half of the seedlings planted survive until they are full grown.
- Plot points on a graph. Connect points. Point out that it forms a line.
- Conclude: So class we can see that there is not just one solution to an equation. There may be infinitely many. In fact, every point that is on the line we just graphed is a solution.
y=(1/2)x

x 1/2x y
-5 -2.5 -2.5
-3 -1.5 -1.5
-1 -0.5 -0.5
1 0.5 0.5
3 1.5 1.5
5 2.5 2.5
7 3.5 3.5
9 4.5 4.5
11 5.5 5.5
13 6.5 6.5
15 7.5 7.5
17 8.5 8.5
19 9.5 9.5
21 10.5 10.5
23 11.5 11.5
25 12.5 12.5

We would have the students to create tables either on Microsoft Excel or TI-82 graphing calculator.

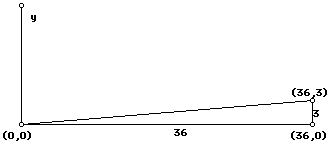
horizontal change
slope = change in vertical units/change in horizontal units. Explain.
slope = 3/36 = rise/run

- Questions to ask at this point are:

1) What other objects have slope ? ( hills, roads, ladders )
2) Can we measure these slopes ?
3) How would you measure these slopes ?
- At this point we will refer back to the graph of y = 3x+1.
Does this line have a slope ?

- Tell the students that slope is constant for linear equations.
(Demonstration from G.S.P )
- Then draw triangles representing rise and run:

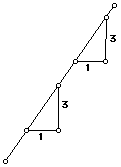
- Reinforce this by looking at table and unit changes of x and y (always stays constant).
- Show the example y= 3x/2 + 2.
- Show that slope is the difference in y-coordinates over the difference of corresponding x coordinates. Make sure that the students know the formula will not work if the variables are changed around.
- Introduce lines with slope zero and no slope.

Misconceptions for slope
- only two points on a line determine slope

Possible uses of technology
- use the TI-82 to show graphs

Assignments
- pp 306-307 1-3, 7-17 odd. 22, 32
- possible practice worksheet

This is the graph of y=2x. It has a slope of two and passes through the point (2,4).

2)

This is the graph of y=4x. We can see that the graph is increasing at a greater rate.


3)

This is the graph of y=(1/2)x. We can see that the graph is increasing at a lesser rate.

4)

This is the graph of y=-5x. We can see the graph is now decreasing.

5)

This is the graph of y=0x+3. We can see that a graph with a slope of 0 is horizontal.

Day 9

---

Day 10

We can see that the y-intercept is 6.

2)

This is the graph of y=3x-4. We can see that the y-intercept is -4.

3)

This is the graph of y=3x+1. We can see that the graph shifted up.

4)

This is the graph for y=3x-7. We can see that the graph shifted down.

5)

This is the graph for y=3x-3. We can see from this and the other graphs that when b is negative, the y-intercept is negative.

6)

This is the graph for y=3x. We can see that it passes through the origin.

Day 11