
Area Explorations
by
Greg Huberty

Area is defined as the amount of space a figure takes up in a two-dimensional
closed figure. This space can take the shape of a square, a triangle, a
rectangle, a circle, or any closed figure. To tell someone what the area
of this figur is depends upon what units you use. For example, a figure
might have an area of nine square feet to one person or one square yard
to another depending on the units that are used. So to find the area of
any figure you must have the units you want. To start, let's use this square
as our unit.
This square is one-half inch on each side. Cut out a square of this size
from the paper your instructor provides. Given this square, how many of
these squares will it take to make up this larger square?

If you put the smaller square into the larger you will see that it will
take four of the smaller squares to make the larger. So we can say that
the area of the larger square is four square units.

Using that same unit, find the area of these next two shapes.


Notice as the figure gets bigger, it becomes more and more work to find
out how many little squares it takes to make up the larger figure which
might be a square, rectangle, or other figure. If you could see the outlines
of the smaller squares and where they would fit into the larger square,
this would make the problem easier.

Then you can simply count the squares to come up with an area of 16 square
units.
But even this can become time consuming if the figure gets large enough.

This is when a formula would come in handy. How many square units do
you count in the large square above? Look here for the solution.
So if you were trying to find the area of something very large such as the
area of a football field to know how much grass needed to be planted, you
need an easier way.
Notice on one of the early figures we looked at the lines show exactly how
much space is taken up.

Notice that this figure has two rows of two squares each and it also
has two columns of two squares each. Look in this next figure and tell how
many rows and columns.

Notice that this time the figure has two rows of three and three columns
of two. Is there a way that we can use this information to make a generalization
about the area of this shape (a rectangle)?
Look at a figure that is a little bit larger and see if your conclusion
works.

Notice that you have two rows of six or six columns of two. The area
by simply counting the squares is 12 square units. How do the numbers that
you got for the columns and rows compare to the area? If you need help look
here.
Therefore the area of a rectangle is the number of rows (width) multiplied
by the number of columns (length).
Try these examples:
Example 1
Example 2
Example 3
What figures will this conclusion work for?
Since a square is a special rectangle, will this conclusion work for all
squares? Justify your answer.
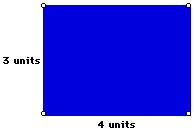
Using the area of a rectangle, what would this area be?
How could you cut this rectangle so as to make two triangles? Use the segment
icon on the screen in GSP to draw the segment you think would create two
triangles. GSP.
What is true about the two triangles that you just made?
Look at the rectangle now with the grid showing the area. Can you tell what
the area of the triangles would be now?

Hint: Move the pieces around so they make whole squares
To see this if you are having trouble click here.
If you need more help try this diagram.
So the area of each triangle [?] is square units. Notice that this is half
of the area of the rectangle we started from, meaning that the line we drew,
the diagonal, cut the rectangle in half.
So the area of a tringle is one-half the area of a rectangle.
Since the area of a rectangle is length times width, then the area of a
triangle must be 1/2 the length times the width.
Using this find the area of each of the following triangles.
Example 1
Example 2
Example 3
Not all triangles are formed by half of a rectangle. Look at these examples.

How can we find the area of these triangles? Why are these different?
After you have thought for a while, click here to see the yellow
triangle.
Can you generalize where point B can be moved so as to keep the original
area?
To see more on the yellow traingle, click here.
Using this knowledge, try this problem.
From this exploration of the yellow triangle, can you find a formula for
the area of any triangle?
See if this will help.
From this we should see the formula for the area of a triangle.
The area of a triangle is one-half the product of the base and the perpendicular
height or,
Look at the following examples and decide whether there is enough information
to find the area and if there is find the area.
1.
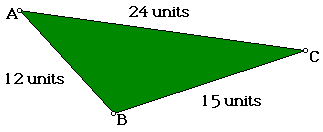
2.
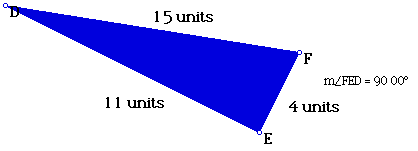
3.
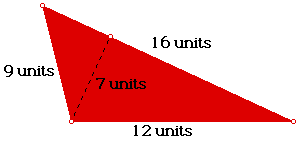
Solutions
Here are some other area formulas to explore.
Area of a trapezoid
Area of a parallelogram
Back to Greg