The students have solved the bank business problem in the first day activity. They are supposed to have a concept of an exponential function and its growth. Today's class is more theoretical. It is to have a knowledge of the shapes of some exponential functions. In fact, they should guess how the graphs would be when some functions are given to them. In particular, if the students are asked to solve some problems about maximum and minimum, this kind of knowledge will be critical in their mind. The students are encouraged to use Algebra Xpressor. In the past, students were dependent on pencil and paper drawing. The same basic concept is alive in this activity among the students. But they should take advantage of the technology and, in addition they will have more exact knowledge from examining the graphs which are drawn by Algebra Xpressor.

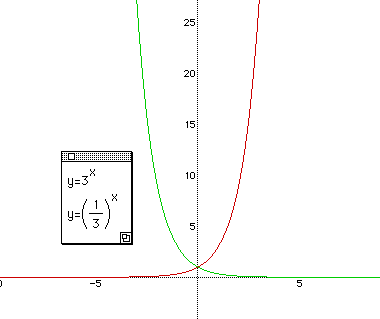
Question 1 : Draw y = ax when both a>1 and 0<a<1. Choose a as a number that you

want to examine.

Student Activity : Since the value of a can be varied, students will be able to do a

creative job. The next graph is drawn with a=3 and 1/3.

The students are asked some questions. (1) What is an increasing function and what is a decreasing functions? (2) What is the relation of two functions? (3) Do they know that (1/3)x = 3-x ? (4) What is the coordinate of the point where two graphs intersect each other?

The teacher should explain the reflection of a function to the y-axis.

Question 2 : Draw the graph of y= ax for several cases of a and make a conjecture of their

increase rate.

Students Activity : The students will be able to examine each case with Algebra

Xpressor. The next is an example.

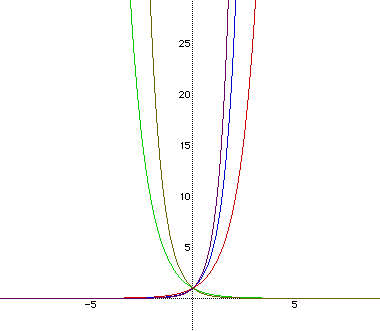
It is important for the students to know the difference from the various value of a.

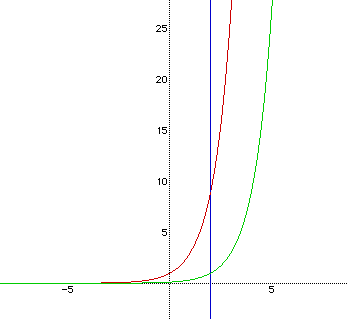
Question 3 : Make students conjecture the graph of y = 3(x-2) . The purpose of this question is to see whether the students can understand the translation of the graph. Make them compare the graphs of two, y= 3x and y = 3(x-2) .

Student Activity : Students try to sketch the graph on a paper. Then they will check the

result. Following is an example.

Question 4 : (1) Draw the graph of y=2ixi. (2) Understand the characteristics of it.

Student Activity : The students are asked to think about the absolute value first, then

they draw the graph and see that what kinds of graphs can make it.

They will know that the graph is the sum of parts of the graphs of

y=2x and y=(1/2)x .

Question 5 : What is the graph of y=1/2(3x +3-x ) ?

Student Activity : They are encouraged to think about the mean of two numbers. Then they will be able to split the given function into y=3x and y=3-x .

Now, the students obtain a graph which may look like a quadratic function. But it is understood that the graph is not a quadratic function, but a combination of two exponential functions. In a sense, the graph is the mean of two values from the two exponential functions.

Question 6 : What is the graph of y=1/2(2x -2-x )? Can you make a conjecture of the graph

before you draw it with Algebra Xpressor?

Students Activity : Students are encouraged to think of each component of the function

first, then they will be able to have a more systematic knowledge.

So there is no harm for the students to use a technology now.

Two different thought can be come up. If a student thinks of two different functions like y=2x and y=2-x and their difference, then the first graph is drawn. But a students thinks of the sum of two functions like y=2x and y=-2-x , then the second graph is more likely.

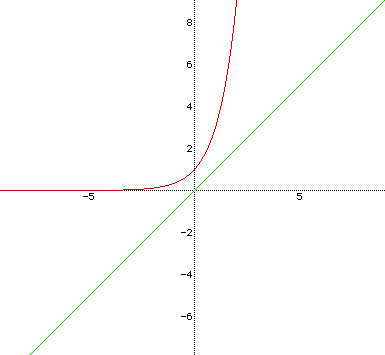
Question 7 : What if you reflect y=3x to the y=x?

Student Activity : The students will investigate a reflection of the function to y=x. They will obtain another interesting shape. The graph has the domain of the positive real numbers andthe range of all real numbers. If they are careful enough to compare these values with those of the exponential function, then they will have a concept of the inverse functions. This activity will be a further exploration.

The second day activity may seems to be too much theoretical. But this activity is designed to bring the students some deep knowledge which is not easy to be transmitted without the help of technology. Teacher has a deciding vote to have this second day activity in his or her classroom.