Activities Using Rational Functions

The following activities deal with rational functions. The materials needed include: springs, spring balances, gram weights, number balance or simple lever, calculators or computers, and centimeter graph paper.

Activity 1 is a one day activity through which students can discover Hooke's law and learn more about linear functions. Before beginning the activity, students should have been introduced to linear functions. That is, they should know that linear functions can be represented in the following general form: f(x) = a - bx, where `a' and `b' are some constant coefficients. The graph of a linear function is a straight line with coefficient `a' representing the point at which the line intersects the y- axis, and coefficient `b' representing the slope of the line.

Activity 1:

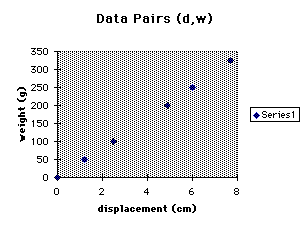
Students will suspend weights from a spring and note the displacement (stretch) of the spring. By recording the weight in grams versus the displacement in centimeters, students will collect data pairs (d,w),where "w" is weight and "d"is displacement, that they can then plot to determine that the relationship is linear. Next, by finding the ratios d/w, they can determine the constant of variation for the spring and the graph, establishing the equation of the linear graph and the constant quotient property of direct variations. Suppose the following is data found by the students.

w (grams)         0        50         100          200        250          325      
d ( cm )          0          1.2          2.5          4.9        6.0          7.7  

The students should graph these data points either on a computer or a graphing calculator. The below graph was done with Microsoft Excel.

Notice that the points seem to form a line.

If we let weight = y and displacement = x, then the line is of the form y = kx. We can use the table values to find k, the constant of variation.

k = w/d = y/x.

The ratios k = y/x are: --, 41.67, 40,40.82, 41.67, 42.21

(The variation of k is due to error in measurement.) Students should find these ratios to determine the constant of variation, k , for the spring.

Now have the students choose an appropriate value for k and graph the equation y = kx to compare with the graph of their data points. One procedure students could use for doing this, called the eyeball fitting technique, requires that they plot the data on a scatter diagram (see above graph) and then use a ruler to draw what they feel is the straight line that most accurately displays the linear trend of the data.

Below is a chart and graph of y = (41.27)x from Microsoft Excel..

 y = weight       x =       
              displace-men  
                   t        
     0        0.00          
     25           0.61      
     50           1.21      
     75           1.82      
    100           2.42      
    125           3.03      
    150           3.63      
    175           4.24      
    200           4.85      
    225           5.45      
    250           6.06      
    275           6.66      
    300           7.27      
    325           7.87      
    350           8.48      
    375           9.09      
    400           9.69      

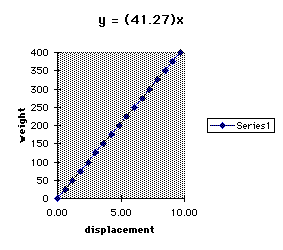
Unfortunately, the eyeball fitting technique may not always give the line which best fits the data. Using this method, two students using the same set of data might each come up with a different prediction equation. Linear regression and the method of least squares can be used to find the best equation ( the least squares equation) to fit the data. Students can be taught to use a calculator or computer to find this equation.

Students should understand how x and y are related in the above graph. Given an x value or a y-value, students should be able to find the corresponding y or x- values. They should also understand that in our equation y = kx, k is the slope of the line and the y- intercept is (0,0).

Once students have an equation representing the data, they should answer questions such as the following:

1. If the displacement is 5 cm, what is the weight?

2. If the weight is 160 g, what is the displacement?

3. If k = 35, what would the graph look like? Explain how the relationship between x and y has changed from the first graph.

Other questions could include unit conversions. For example, "if the displacement is 2 inches, what is the weight in grams ?" (given a particular spring constant k).

Now have the students repeat the experiment with a stiffer spring and then with a softer spring. The displacements will be smaller with the stiffer spring, giving K a larger value. Similarly, softer springs will have smaller K values. By plotting data as done above, students should observe how the slope changes depending on the stiffness of the spring. (And how this change in slope affects the relationship between x and y.)

The above activity would be good for a mathematics class or a physics class to do. A physics class could concentrate more on the physics behind the experiment. An explanation could follow the experiment. (See below.)

Explanation:

Let F be the force exerted by the spring. Then F = -kx, where x is the displacement of the body (weight) from its unstretched (x = 0) position. K is a positive constant called the force constant of the spring. This force law for springs is known as Hooke's law.

Force exerted by the spring is always directed opposite the displacement. The force of a spring on a block (or weight) varies with the block's displacement from the equilibrium position (x = 0). When x is positive (stretched spring), the spring force is negative. When x is zero, the spring force is zero (natural length of the spring). When x is negative (compressed spring), the spring force is positive.

In our experiment, x was positive (stretched spring), so the force was negative. Thus, we get -F = -kx (or F = kx).

Activity 2: The following activity can be done the day after activity 1 is completed.

The number balance contains pegs equally spaced from the fulcrum and from which weights can be suspended. Have students suspend a 200 g weight from a peg 5 units (left) from the fulcrum. Next, have students use a spring balance to exert a force from different pegs on the other side of the fulcrum sufficient to balance the 200 g weight on its 5-unit moment arm. Students will record data pairs (Dr,Fs) representing the (right) distance Dr of the spring from the fulcrum necessary to achieve a balance (raise the weight on the other end of the lever) and the spring force Fs in Newtons.

Have the students plot data pairs. The goal here is for students to discover the shape of an inverse variation relationship (as the distance Dr increases, the amount of force Fs decreases). Possible data may be as follows:

Dr          1           2           3           4           5           6           
Fs          9.0         4.5         3.0         2.25        1.8         1.5         

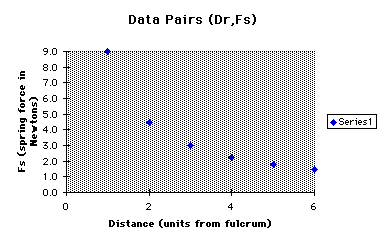
Now have students find the product of each data pair to establish the constant product property of inverse variations and the constant of inverse variation.

k = (Dr)(Fs) = 9.0 for each data pair.

k is the constant of variation.

k = (Dr)(Fs) implies that Fs = k/(Dr). This is an inverse variation.

Students should draw a curve through their data points. They should note that the curve is approximately y = k/x, where y = Fs and x = Dr. The following graph is of y = 9/x. This equation (graphed in Algebre Xpresser) should be compared to the above graph (of data points).

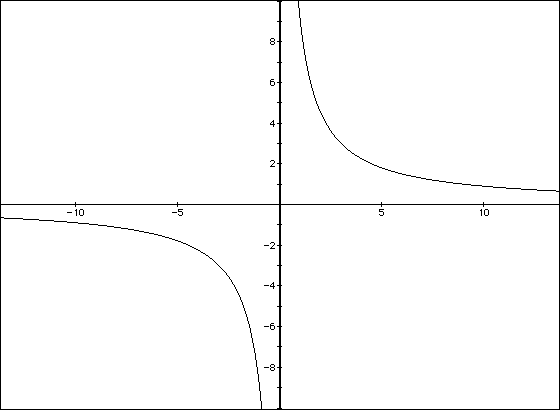
The part of this graph where x is positive corresponds to the above plot of data points. This is because our x is the distance Dr the spring is from the fulcrum. (This distance is never negative.)

The below picture was made using The Geometer's Sketchpad. It shows a number balance with a weight on the left side and a spring balance on the right. Students can exert forces from different pegs on the right side of the balance. And after experimenting with a stationary weight, students can experiment further by changing the location of the weight.

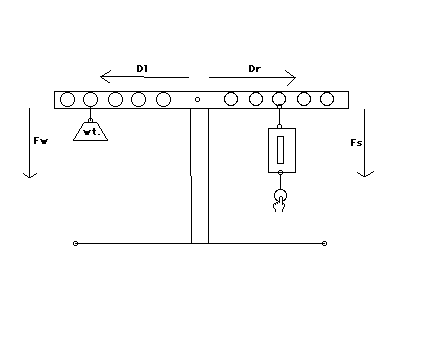
In the above picture, Dl represents the distance the weight is from the fulcrum. (In the picture, Dl=4 since the weight is on a peg 4 units from the fulcrum.) Similarly, Dr represents the distance the spring balance is from the fulcrum. Fw is the force exerted by the weight, and Fs is the force exerted by the spring balance (due to the student's pulling on it). The force the students use on the spring balance should be enough to balance the weight (on the moment arm).

By experimenting with the locations of both the weight and the spring balance, students can discover Varignon's theorem, one of the most useful principles of mechanics. This theorem states that the moment of a force about any point is equal to the sum of the moments of the components of the force about the same point. Another way of saying this is that the sum of the moments (products of force and distance) about the fulcrum equals zero. A physics class could go deeper into the meaning of this theorem. (See the below explanation.)

-(Fs)(Dr) + (Fw)(Dl) = 0 (Use the "right- hand rule" to determine signs.)

(Fs)(Dr) = (Fw)(Dl)

Fs = (Fw)(Dl)/(Dr)

Fw = (mass)(acceleration), so for a 200 (g) weight, we get:

Fw = (0.200 kg)(9.8m/sec2) = 1.8 Newtons, so

Fs = (1.8 Newtons)(Dl/Dr)

For example, if Dl = 5 and Dr = 3, Fs = (1.8)(5/3) = 3 Newtons.

If the weight was stationary at 5, then Fs = k/Dr, where k = 5(1.8 Newtons)

Now let's look at possible results from the student's changing the location of the weight if the spring balance is stationary at unit 3 (Dr = 3).

     Dl            1        2             3             4             5             
     Fs           0.6       1.2           1.8           2.4           3             

Students can now plot these data pairs.

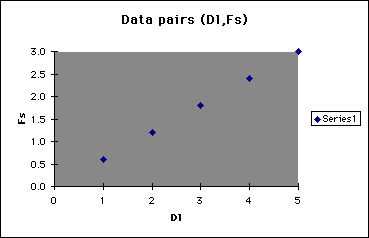
From the plot, it looks as if Dl and Fs are linearly related when the weight amount (mass) and the location of the spring balance are constant.

After students have done several experiments, they should be asked to explain some of their results. For example, from the above plot, they should see that as the weight goes farther away from the fulcrum, more spring force is needed in order to balance the arm of the number balance. They should also be able to answer questions such as the following:

Given a weight of 200 g, if Dl = 3 and Dr = 4, what is Fs?

So far in this activity, Fw has remained constant. Students can further experiment by changing the weight. Weights of different amounts should be given to the students for experimentation. They can first experiment with a stationary weight and spring balance, and then again by changing the location of the weight or spring balance. For each experiment, data points should be plotted and conjectures should be made. For example, students should note that if Dl = Dr, then Fs = Fw.

References

National Council of Teachers of Mathematics. (1992) Curriculum and Evaluation Standards for Mathematics. Hirsh, Christian R: Editor.

Serway, Raymond A. (1990) Physics for Scientists and Engineers (3rd Ed.) CA: Saunders College Publishing