What does a mathematics teacher have to think about his teaching mathematics?
The professional standards for teaching mathematics (1989) says that, "helping
students develop mathematical power takes tools, resources, and experiences
very different from previous practices" ( p. 179 ). If a teacher is
asked to find ways to provide appropriate resources for teaching mathematics,
what does he have to do? At least, he would not assume that he has enough
resources just with his mathematics textbook and some other reference books.
HiMAP ( High School Mathematics And Its Application ) project is in gear
with the Standards in many ways. The goal of HiMAP is to develop a system
of instructional modules in high school mathematics and its applications
that may be used to enhance teacher training at the secondary school level.
As clearly stated, HiMAP is intended for mathematics teachers. After review
by a teacher, the materials are meant to be used in the classroom as a supplement
to the textbook. HiMAP is funded by the National Science Foundation to the
Consortium for Mathematics and Its Applications ( COMAP ), Inc., a non-profit
corporation engaged in research and curriculum development in mathematics
education. COMAP ( Consortium for Mathematics and Its Applications ) which
is the mother project of HiMAP is dedicated to the improvement of mathematics
education for every layer of society from elementary and secondary schools,
two-and four-year college, industry, and government. HiMAP is one of the
projects of COMAP for high school mathematics and its applications.
HiMAP made me interested in exploring its content since I have not seen
a project or educational material mainly for teachers' use. In fact, I have
been exclusively exposed to the importance of students' learning and development
of materials for the students. Teaching is a complex interaction between
the teacher, the content to be taught, and the students, therefore in a
radical sense, one important factor of teaching has been missing. Though
there has been an effort by mathematics teachers themselves to return to
the universities to pursue graduate programs in mathematics education, it
seems that universities are taking most of the role of continuing teacher
education. So the value of HiMAP is highlighted because HiMAP will be able
to allow mathematics teachers to have experience in educating themselves
so that they may deepen their knowledge and skills in teaching of mathematics.
HiMAP consists of 22 different modules and they look easy to integrate
into the present curriculum. For example, if a teacher wants to talk about
the use of mathematics in social issues to his students, he will be able
to refer to the module 19, Fair Voting: Weighted Votes For Unequal Constituencies.
He will be able to not only explain how power can be measured quantitatively,
but also show his students how mathematics can include problems from within
and outside of mathematics. Some modules are supported by a video program
so that students' understanding about these topics can be strengthened.
One of the 22 modules entitled Applications of Geometrical Probability
is the main focus of this paper. Applications of Geometrical Probability
does not have a video program but focuses on providing mathematics teachers
with many applicable resources in teaching probability. Applications of
Geometrical Probability is composed of examples, black-line masters for
transparencies and supplemental exercises with solutions. The examples are
mainly real-life problems and show how to solve the probability problems
with their geometrical models. Mathematics teachers should decide the use
of the problems presented in the module and expand their areas, since the
module is only 19 pages long and doesn't tell everything that the teachers
need for further explorations.
The examples in the module have suggested lesson plans for mathematics
teachers so that they can try to solve the problems first and find other
creative ways. Just as students are encouraged to experiment and estimate
when analyzing probability problems, and use their estimates to develop
models that simplify a complex real-world problem, HiMAP asks the same activity
of the mathematics teachers. Teachers need to learn mathematics in a manner
that is consistent with the way we expect them to teach and this idea is
reflected in the HiMAP modules.
Group and individual exercises are prepared and those are ready to be photocopied
at the end of the module. It is interesting that the counting principles,
elementary combinatorics, urn problems, and probability of exactly r successes
in n trials, etc., which are well-known types of probability problems, are
not introduced in the module. This can be explained if we consider the author
of the module. Fred C. Djang who has taught mathematics at the junior high,
high school, college and graduate level is a firm advocate of the importance
of application-based mathematics instruction and all the problems in the
module seem to be devised to fit his goal. Students are asked to solve the
probability problems with the knowledge of coordinate geometry, algebraic
manipulation, percent, and conic sections. They are asked to experiment
and estimate the solutions of probability problems by making a geometrical
model. The first process to a solution is making their own model.
"Geometrical probability" can be described as conducting
a real-world experiment for which outcomes can be represented by points
in a geometric region. So the desired probability is considered as below:
Measure of the Feasible Region
Probability = ----------------------------------------------------
Measure of the Sample Space .
The author talks about geometrical modeling as a way to reconstruct a problem.
For example, consider throwing darts at a dart-board that is one unit square
and has a circle of radius 1/10 unit. What is the probability that the dart
will land within the circle assuming that throws would be distributed equally
throughout the dart-board? The probability of the dart ending up in the
circle is equal to the area of the circle divided by the area of the square.
Since the area of the square is 1 and that of the circle is [[pi]](0.1)
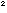 , the desired probability is (0.01)[[pi]]. Once students can make
a model to solve the probability problem, the model becomes powerful in
simplifying a complex problem. (figure 1)
, the desired probability is (0.01)[[pi]]. Once students can make
a model to solve the probability problem, the model becomes powerful in
simplifying a complex problem. (figure 1)
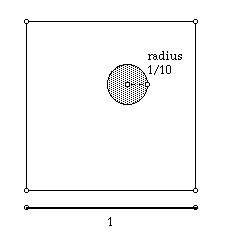
figure 1
The next example is a typical type of problem that students can often see
in their algebra class. How can it be applied in learning probability? The
module tries to show students how coordinate geometry and algebra are related
and applied together.
What is the area of intersection when 0<x  1, 0<y
1, 0<y  1,
and x+y>1 ?
1,
and x+y>1 ?
But, Applications of Geometrical Probability offers the same problem following
way.
Peter and Paul are very good friends who decide to set up a joint
checking account. Each one puts in 50% of the initial deposit. They
trust each other and have agreed that if one should need to spend
more than his share, he is allowed to do so. Sure enough, such an
occasion occurs when the two boys are shopping for Christmas gifts.
Unknown to each other, they both write checks. What is the
probability that they have overdrawn the account?
If students can represent the amount of Peter's check as the x-axis,
and that of Paul's check as the y-axis, then they will know that how the
first short problem with numbers and symbols changes into the second word
problem. Though the two problems require the same mathematical knowledge
in solving them, the reasoning and problem solving skills needed are very
different. The desired probability would be 1/2. (figure 2)
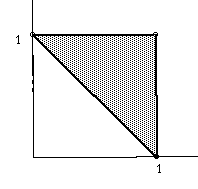
figure 2
The problem requires teachers to know the relationship between verbal representations
and their symbolic notation. Teachers also have to be able to explain the
consistency when they exchange Peter's check as y and Paul's check as x.
In addition, if the same scenario occurs with another friend, Mary, the
problem is extended to a three-dimensional graph with the z-axis representing
Mary's check. Since being able to draw a shape shows having spatial sense,
this kind of activity should be recommended by mathematics teachers. Students
will be able to explore a three-dimensional figure with ease in this kind
of problem set. One question aroused is whether a teacher has familiarized
these approaches to use the module to its best potential. In particular,
in this extension, the probability that an event does not occur is 1 minus
the probability that it does occur can be understood easily by the visualized
model. As indicated below, it is easier for students to look at the region
that is not shaded. The region is a pyramid whose volume is 1/3 the area
of the base times the height, or 1/6 of the cube. Students can conclude
that the probability of being overdrawn is 5/6. (figure 3)
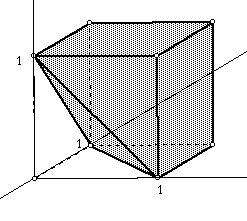 figure 3
figure 3
The other examples in Applications of Geometrical Probability which are
not presented in this paper include a wide range of mathematics from algebra,
geometry, trigonometry even to calculus. So the probability problems are
not confined to one specific topic. They broaden the area of problems. It
means that HiMAP asks mathematics teachers to have a broad knowledge of
the entire high school mathematics curriculum. This benefits students because
they can be offered more mathematical knowledge by their teachers and experience
mathematics for themselves. Repetitive routine problems is deemphasized
in the module.
The next example is entitled Paradoxes. To me, it is the most exciting
problem in the module. The problem shows that three different solutions
can show up for a probability problem and no one can tell which answer is
right. The validity of the answers depends on the three different geometrical
models that students generate. Therefore, students can be motivated to explore
the other solutions and find the reasons for them.
Given a circle with diameter 2, what is the probability that the length
of a chord drawn will exceed 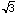 ?
?
Model 1
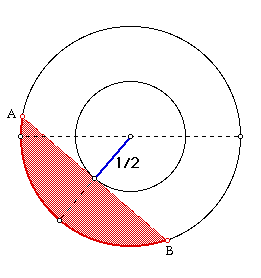
In Model 1, the radius of the inside circle is 1/2 and that of
outside circle is 1. Thus, we have the length of half of the chord
is 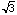 /2 by the Pythagorean Theorem. So we obtained
/2 by the Pythagorean Theorem. So we obtained 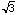 as the length
of the chord. If the chord passes through the inside circle, then
the length of AB will exceed
as the length
of the chord. If the chord passes through the inside circle, then
the length of AB will exceed 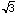 . If the chord does not pass through
the inside circle, then the length of AB is less than
. If the chord does not pass through
the inside circle, then the length of AB is less than 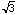 . Here, AB
is tangent to the inside circle and we can rotate AB around the
inside circle.
. Here, AB
is tangent to the inside circle and we can rotate AB around the
inside circle.
Area of the Inner Circle
Probability = --------------------------------------
Area of the Outside Circle
= 1/4
Model 2
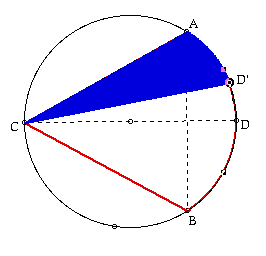 In this model, the endpoint, D', of
In this model, the endpoint, D', of
In this model, the endpoint the chord CD' can be moved along the circumference of the circle from the
fixed point C. Since any angle inscribed in a semicircle is a right
angle, we have that ACD is a right triangle. Thus, if the angle ACD is
[[pi]]/6, then the angle ADC is [[pi]]/3. So, now we can apply the
relationship between the ratio of the three angles [[pi]]/3, [[pi]]/6, and
[[pi]]/2 and that of the three lengths 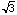 , 1, and 2, respectively. Since the
diameter of the circle is 2, we have the length of chord AC is
, 1, and 2, respectively. Since the
diameter of the circle is 2, we have the length of chord AC is 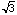 . We have
the desired probability when the chord CD' moves along the arc ADB.
. We have
the desired probability when the chord CD' moves along the arc ADB.
Length of Arc ADB
probability = -----------------------------------
Circumference of the Circle
= 1/3
Model 3
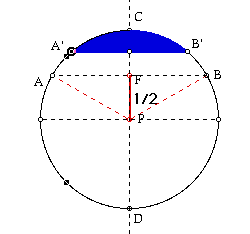
In this model, the chord A'B' is perpendicular to the diameter CD. As
the chord A'B' moves from the point C and down to the chord AB. Since the
length of PB is 1 and length of FP is1/2 the length of the chord A'B' is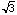 .
The Pythagorean Theorem gives us BF is
.
The Pythagorean Theorem gives us BF is 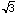 /2 and hence AB is
/2 and hence AB is 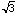 . The desired
probability is obtained when the chord A'B' starts moving from AB to the
point P.
. The desired
probability is obtained when the chord A'B' starts moving from AB to the
point P.
Length of FP
probability = ----------------------------
Length of CP
(1/2)
= ----------------
1
With these three interpretation, students can obtain three different
solutions. Of course, a teacher should be able to understand the meaning
of the problem and its solution process in each model. This problem is nicely
made. Students can use their knowledge from high school geometry in solving
the problem. The diameter of the circle is 2 and the length of the chord
is 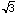 , and the numbers and the theorems that are used in each
model are familiar to the students. They learned all knowledge from their
geometry class. Mathematics is not just a subject that requires a formula
for a problem any more. The students obtain the three right answers so they
can see that mathematics does not require a right answer all the time. Most
of all, this problem is totally different from the other problems that students
have encountered so far. Further the teacher may end up with more creative
models and their solutions by his students. This will please the teacher.
After this activity, the teacher can go on to explain that in any experimental
design, the results are subject to human bias. Not only should students
be encouraged to find other approaches which generate other solutions, but
also teachers should be encouraged to develop extensions to the problem.
It is important for the students to know that mathematics is not about formulas
and an exact answer to a larger extent.
, and the numbers and the theorems that are used in each
model are familiar to the students. They learned all knowledge from their
geometry class. Mathematics is not just a subject that requires a formula
for a problem any more. The students obtain the three right answers so they
can see that mathematics does not require a right answer all the time. Most
of all, this problem is totally different from the other problems that students
have encountered so far. Further the teacher may end up with more creative
models and their solutions by his students. This will please the teacher.
After this activity, the teacher can go on to explain that in any experimental
design, the results are subject to human bias. Not only should students
be encouraged to find other approaches which generate other solutions, but
also teachers should be encouraged to develop extensions to the problem.
It is important for the students to know that mathematics is not about formulas
and an exact answer to a larger extent.
When evaluating the students, the teacher should look at the students'
activity carefully and decide the reasonableness of the students' outcomes
because the module provides teachers with many factors with that they can
evaluate their students. The active involvement of students in the process
of problem solving is emphasized. Thus, "knowing mathematics is doing
mathematics" is realized. The module is full of good exercises that
can bring many different approaches to mathematics classroom. So the students'
attitude toward mathematics is likely to change.
The effectiveness of HiMAP can be thought about in different ways. The
executive director of COMAP, Solomon A. Garfunkel, said that he feels strongly
that HiMAP's efforts have succeeded, and that more and more of the ideas
of HiMAP project have found their way into mainstream text books and into
new more comprehensive curriculum projects. Moreover, he commented that
the NCTM standards reflected in a great deal of influence on the mathematics
education community. If I could have obtained data about how many high school
teachers are using HiMAP modules, I would feel better in telling that HiMAP
did many things in helping teachers to present more applications. Because
material alone is not sufficient in evaluating the success of a project.
Norm Webb who is a professor of the university of Wisconsin and did a summative
evaluation of nine projects including HiMAP for NSF said that HiMAP was
a good project in completing the goal of the development of material, but
commented that HiMAP had a dissemination problem as well as the other eight
projects did.
HiMAP can be a success in a way that the quality of the mathematics teacher
is emphasized as much as that of students and material since the quality
of the curriculum and the skill of the teacher both are vital. HiMAP strove
toward its goal of providing a professional environment in which classroom
teachers could actively participate in the mathematics education. In the
students' perspective, HiMAP can provide more significant, challenging subject
matter interestingly and meaningfully taught. In the teachers' perspective,
HiMAP can be a good mirror where the teachers should analyze and evaluate
the appropriateness and effectiveness of their teaching. In particular,
if a teacher does not feel comfortable in teaching probability, he may be
able to find himself interested in the problems in the HiMAP modules and
further more, he will try to take some of the problems in his mathematics
classroom. Then the effect of HiMAP will go to the students through their
teacher.
Finally, I hope that a connection to statistics should be considered in
the further development of HiMAP modules and new mathematical fields should
also follow.
References
Fred C. Djang. (1988). Applications of geometrical probability. Lexington,
MA.
Garfunkel, S. (1994). For all practical purposes: Introduction to contemporary
mathematics (3rd ed.). New York: Freeman.
National Council of Teachers of Mathematics. (1998). Curriculum and evaluation
standards
for school mathematics. Reston, VA
National Council of Teachers of Mathematics. (1998). Professional standards
for teaching
mathematics. Reston, VA.




 In this model, the endpoint, D', of
In this model, the endpoint, D', of 