Exploration : How to Derive a Parametric Equation for a Curve

C

t

K P

L R O

Let's begin with the discussion of the figure given above. Our aim is to obtain a parametric equation using the above presentation.

Here is the explanation of the figure given above, a dotted circle shows the previous position of a circle, and O is the initial position of a fixed point . The position of the fixed point is initially at the origin. The circle is rolling towards the negative x-axis. After the circle takes OL units on the line, the new position of the circle is given by the blue circle, and the point P denotes the new position of the point we are tracing. The tracing path of the fixed point on the circle is shown by a dark blue arc, between PO. L is the point of intersection of the later position of the circle and the line. The point C is the center of the circle. R and K are the legs of the perpendicular segments drawn from P to the segment OL and CL respectively. Finally, t denotes the angle <PCL. We are going to find the parametric equation which corresponds to the path.

Let's consider the next facts. While our fixed point is moving from the point O to the point P, how long distance does the circle move on the line?

We can observe that the length of the segment OL is equal to the length of the arc PL, since the point O came to the point P after the circle rolled OL units on the line.

this fact implies that OL has the length r t.

Can we find the arc PL in terms of the radius of the circle ? (where the radius of the circle is r) Yes, we can. The length of the arc AB is equal to rt.

If we think of the coordinates plane of x and y, the x-component of point P is equal to length of the segment OR, or x= OR which is equal to OL - RL. Now we have x = OL - RL.

From the previous discussion, we know that OL = PL. Then x = PL - RL.

We have also another equality PL = r t. Examining the trapezoid RLCP, RL = PK and PK = r sin t.

Therefore,

x = r t - r sin t.

Similarly, the y- component of the point P is equal to PR. It can be directly found that PR = KL. Hence, y = RP = CL - CK.

We know that the length of the segment CL is r unit, and the length of the segment CK can be found from the right triangle PCK. PC = r and the angle <PCK = t imply that r cos t.

Therefore,

y = r - r cos t.

Because the both equations depend on t, it is better to write the pair of parametric equations in the following way.

x(t) = r t - r sin t and y(t) = r - r cos t .

So we have derived the parametric equation of the curve defined.

Let's see the graph of the parametric equation. We can refer the next figure first. Tracing of the point on the blue circle makes the graph of the equation.

So, it will be an arch shape and the length of the arch is same with the perimeter of the blue circle with the radius r. In the following figure, as we mentioned before the blue ones are showing the equation. Then, what are the red and green figures? It is the general case of the graphs of the equation according to the Position of the tracing point. That is to say, if a point is inside of the circle, then it will be red one and if a point is outside of the circle, then it will be green one.

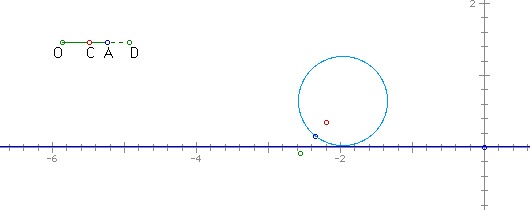
The graphs are taken from GSP. OA defines the radius of the circle, C is the point of segment between the point on the circle and the center of the circle, and D is an outside point on the extension of the segment connection center and the point on the circle.

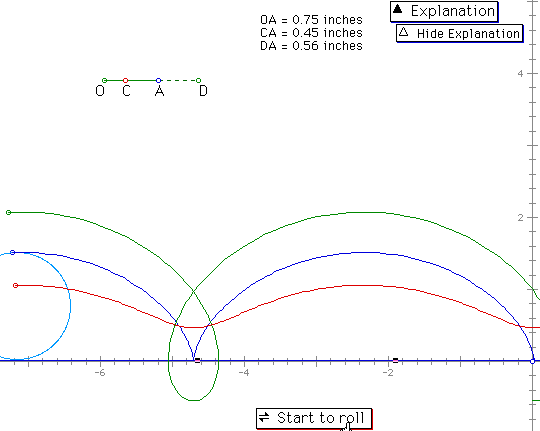
The next is another figure which shows the traces of the three points ( points on the circle, inside the circle, and outside the circle ).

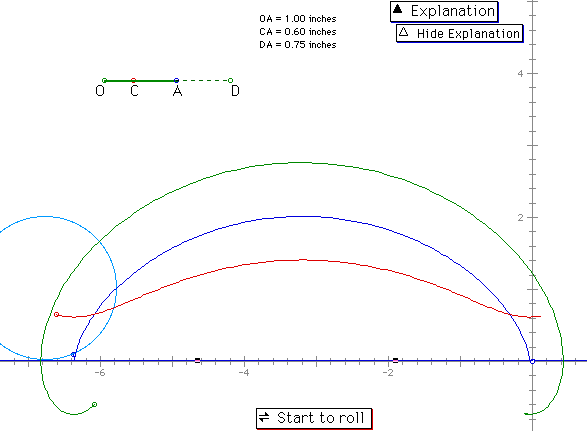
Let's use another graphic program, Theorist. Theorist is one of the good graphic programs which can show the parametric function very well.

Here we need to mention " Cycloid " because the graphs which we are going to observe are cycloid. A cycloid is the locus of points of a point on a circle rolling along a line without slipping.

Let's see the types of cycloid for different radius values. We are going to use the parametric equation, x(t) = r t - r sin t and y(t) = r - r cos t .

For example, when the radius of circle is 2 then the graph is the following. The picture is from Theorist where r = 2, x = r t - r sin t, and y = r - r cos t.

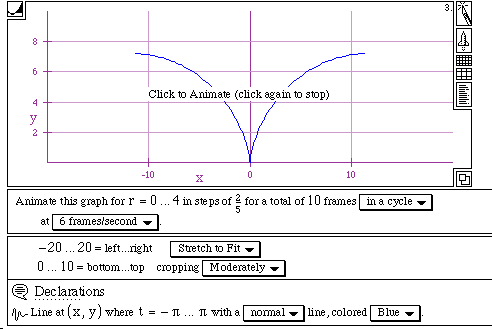
Let's discuss the role of t. Since t is between -[[pi]] and [[pi]], the graph does not show the whole of two half circles. Let's change the range of t into between -2[[pi]] and 2[[pi]]. See the next graph.

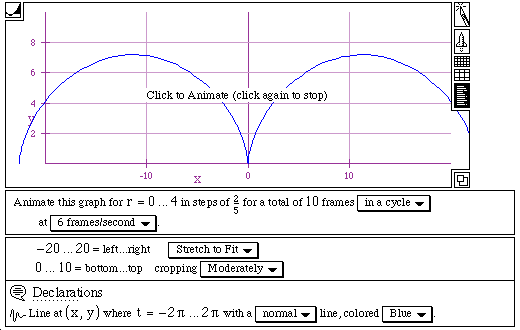
There is another thing that we need to talk about. In the above figure, the graph goes up to near 8 on y -axis since the graph is animated for r = 0 ... 4. What if we change the range of r into r = 0 ... 2. See the next graph.

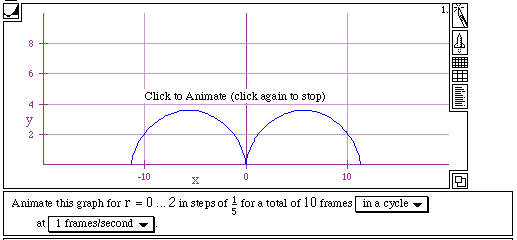
As we can see on the above the graph goes up to near 4 on the y-axis then starts to go down.

Let's think of deriving another parametric equation for the other curve which was mentioned above. If we have an attached point to the rolling circle not on the circumference but at the distance b from the center, the curve obtained from the trace of that point is called a trochoid. The following figure shows the case for b>a and b<a.

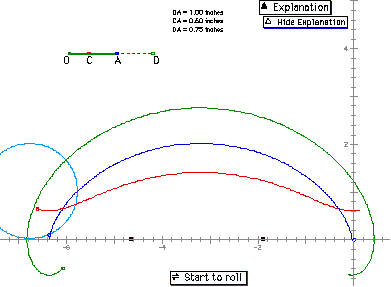
The equation is the modified version of the previous one. The parametric equation of green or red path (trochoids) is x(t)= a t - b sin t and y(t)= a - b cos t. Here b should replaced by b' in the case of red path..

So far we have examined the many interesting things of the parametric function x = r t - r sin t, and y = r - r cos t with GSP and Theorist. They are kinds of extension of the parametric function x = r t - r sin t, and y = r - r cos t which we could derived in the first phase of this paper. Knowing various facts of a function will be able to an inspiration for students to improve their disposition to do mathematics.