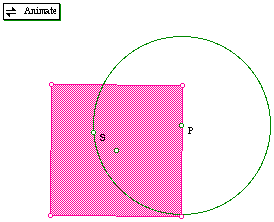
Setup:
The setup for the polygonal problem is, what would happen if a point P was
located on the perimeter of a pentagon. Point P also happened to be the
center of a circle and this circle has a fixed point, S, in which it passes
through that is inside the pentagon. Now let point P travel along the perimeter
of the polygon, and point S will remain stationary and constant. This is
going to form a series of circles that envelope the polygon. This paper
will investigate the results of such a setup.
Geometer's Sketch Pad is a perfectly suited program to investigate this
problem. It have the capabilities to animate point P along the polygon,
and it will trace all of the circles that are formed by this movement. Regular
Polygons were used in order for the results to be easily simulated by other
investigators. Below is an example of how the program is setup, and a square
was used as a random example.

Results:
The following figures are the results of animating P along the perimeter
of the polygon. A equilateral triangle, square, regular pentagon, and regular
hexagon were used in this investigation.

Click here for a Geometer's Sketchpad
file for the equilateral triangle path.

Click here for a Geometer's Sketchpad
square path.

Click here for a Geometer's Sketchpad
regular pentagon path.

Click here for a Geometer's Sketchpad
regular hexagon path.
Analysis:
As we can see, when the point P travels along the polygon a series of circles
are formed. The circles have a radius of the distance between point P and
point S. The sequences of circles form together to emphasize the presence
of more prominent circles. These circles have the center at each of the
vertices, thus the number of prominent circles is the same as number of
vertices. The size of these circles directly relates to the distance between
the stationary point S and each vertex. If S is located close to the vertex,
then the resulting circle will be small, but if S is located on the opposite
area of a vertex then the resulting circle will be large.
What if...
What if S is the center of the polygon? What will happen to the circles
that are formed by P traveling across the perimeter? The following hexagon
is an example of what would result when S was located at the center of the
figure.

When the point S is located in the center of the polygon an interesting
design is formed. The circles that are formed around the polygon with the
centers at each vertex are exactly the same size. In the above example there
are six congruent circles around the hexagon. This can be proven true because
the radiuses of the circles are the distance between the vertices and the
center. A property of regular polygons is that the center of the polygon
is equidistant from all of the sides; therefore all of the circles have
the same radius and are congruent.
What if the point S is on the polygon? What will be the effect on the circles?
Is there a relationship between the sizes of the circles? The following
is also an example of the common results that were found in all of the polygons.

It is obvious to see that the number of circles that are formed are not
changed, there is still one circle for each vertex. However there are two
interesting occurrences. First as P travels along the border of the polygon,
there is one point in which no circle is formed. This is occurs of course
at the point on the perimeter where point S lies. So when S is on the border
there is an instance of an empty set for a resulting circle. Secondly, when
the point S is placed at a midpoint of a side (as seen above), the resulting
circles have a special relationship. The vertices (A,B) that are on each
end of the side that is bisected by S, form circles that are congruent.
This is because the radiuses (distance from each vertices to point S) is
equal, thus the circles are congruent. Also, the vertices that are adjacent
to A and B (CD) are going to form congruent circles also. This can be proven
by showing that the distance of a radius of CS and DS are congruent. When
the line segments are drawn in, it forms two right triangles that can be
proven congruent by SAS. Thus if the two triangles are congruent, then CS
and DS are congruent (CPCTC), and the resulting circles are congruent. This
phenomena holds true for the other polygons, and can be proven so by a similar
proof. Polygons with an even number of vertices will have pairs of sides
that form congruent circles. Polygons with an odd number of vertices will
have result in a circle that does not have a congruent circle.
What if the point P is located outside of the polygon? Will the circles
be within one another? Will there be any new relationship between the circles?
The equilateral triangle was used to illustrate the previous condition.

The resulting figure is very similar to when point S is inside of the
polygon. There are still the same number of circles as the number of sides,
and each circle has a center at a vertices. The circles will change size
depending on the position of point S. If S is collinear with one of the
two vertices that form a side, then one of the resulting circles is inside
of another.

The circle with the center of O is inside of the circle with the center
N, and both of the circles meet only at point S. This occurs because O is
on the radius of circle N, thus meaning that the radius of circle O will
lie also on the radius of circle N. This will produce two circles where
the centers are lined up. The radius of circle O is smaller than circle
N because O lies between N and S.
Finally, what will happen if S is moved a great distance away from the polygon?
This situation is illustrated by moving S away from the polygon, and having
the polygon small. This will simulate the effects of having S a great distance
away from the polygon with respect to its size.

In the above illustration the center of the circle is the polygon that
has been reduced and the point on the right is the point S. As you can see
S is a great distance away from the polygon, with respects to the size of
the polygon. The result of having point P travel across the perimeter produces
the previous figure. There are still 5 circles (the polygon is a pentagon),
but the circles are not as prominent. This is because the distance that
P travels with respect to the location of S is every small. So for all practical
purposes, if S was move even farther away the result would eventually be
five circles that overlap.