When given any two random circles that do not intesect at any point,
or neither circle is inscribed within the other, there are only a few lines
that are tangent to BOTH circles. Let us look at an example:
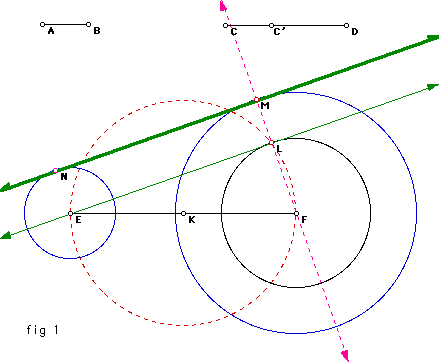
Notice that the dark green line MN is tangent to both circles. This line
was constructed by producing a circle (black) with center F and radius=
radius CD - radius AB. Another circle was constructed (red-dashed) with
the diameter equal to the distance between E and F. The circle K intersects
both point E and the black circle F at one point. A line is draw between
these two points LE. The distance between points L and M is equal to the
radius of AB. Line MN is then constructed to be parallel to LE but simply
moved to be tangent to the blue circle F with a distance of AB away from
EL. By this construction it is now tangent also to circle E. There is another
line tangent to both circles on the opposite side of the circles. Thus there
are two lines on the exterior of the circles. Click here
to have a GSP Sketch of this result.
Now let us look at the case of the interior tangent lines of two circles,
that is, tangent lines for which the two circles lie on opposite sides of
the line:
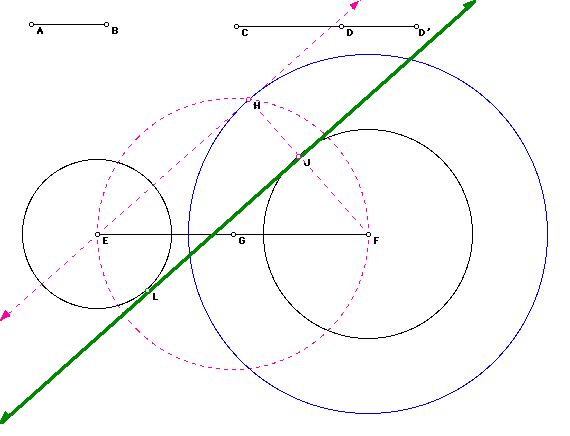
This construction was made in the same way as before with the exception
that the blue circle has the radius of AB + CD (the radiuses of the given
circles). This will generate a line, JL, that is also tangent to both of
the circles on the interior of them. Click here
to have a GSP Sketch of this result. There is another line (not shown) that crosses has
a negative slope of JL and will also be tangent to circles E and F in the
opposite direction. So, there is a sum total of four lines that are tangent
to two, non-intersecting circles.
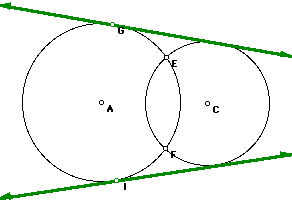
Now let us look at some other possibilities. How many lines of tangentcy
are there to two circles that meet at one point and are not inscribed within
one another.
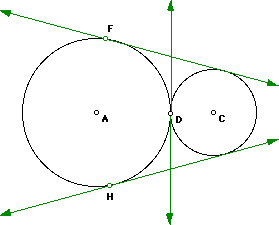
We can see that there are only three lines that intersect both circles,
the two exterior lines and then only one interior line. If the slope of
line D is change just a bit it will interset the circles in two points,
this idea may not be easily seen but considering there is only one line
tangent to a circle at any given point, and the point is one fixed point
on both circle, then there is only one line of tangentcy on the interior
of the circles.
Some other possible extensions to this problem, and their tangent lines
are given:
or....