Marc Lewis and John Moore

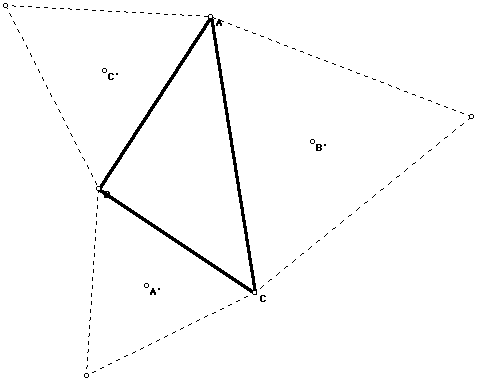
Napoleon's triangle is found when, given any triangle, equilateral triangles are constructed on the exterior of each side. The center of an equilateral triangle can be found by finding the circumcenter, the centroid, or the incenter (note: all of these centers are the same in an equilateral triangle). Below is a triangle ABC with the equilateral triangles and the centers A', B', C':

NAPOLEON FIGURE 1

When the centers A', B', C' are connected, the resultant triangle is equilateral:

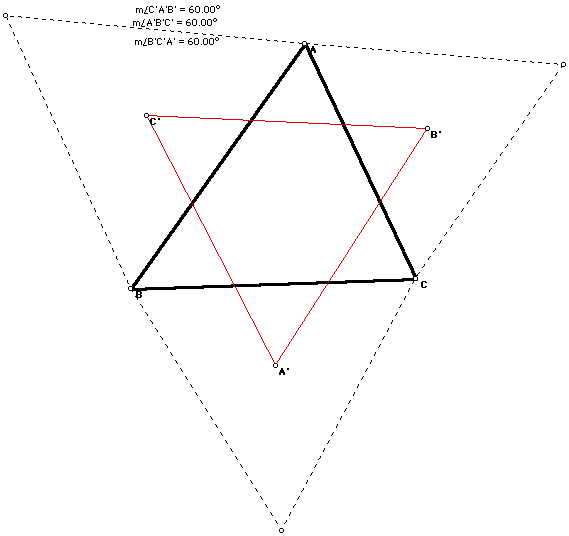
NAPOLEON FIGURE 2

As A, B, C are moved around, Napoleon's Triangle remains equilateral. Why is this? A discussion looking at certain types of triangles might help us find the answer.

The first type of triangle is an equilateral triangle. As predicted, the Napoleon's Triangle is equilateral. However, there is another characteristic that pops up in this triangle:

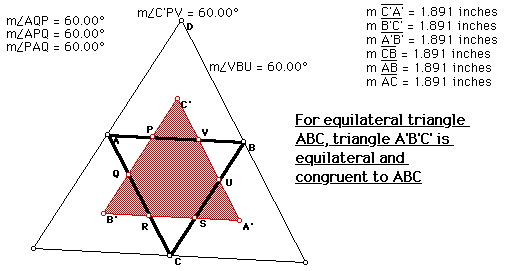
NAPOLEON FIGURE 3

Not only is triangle A'B'C' equilateral, it is also the same size as triangle ABC. In fact, if you take triangle A'B'C' and make it's Napoleon Triangle, you'll get triangle ABC.

Let's take a look at an isoceles triangle. Below is isoceles ABC and it's Napoleon Triangle:

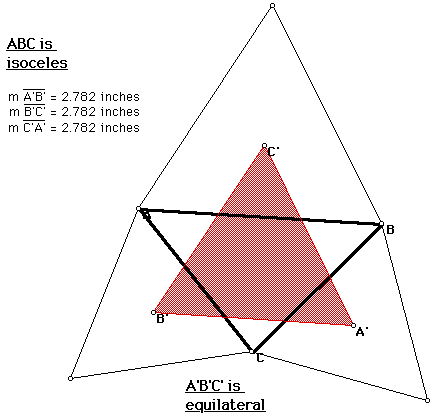
NAPOLEON FIGURE 4

As expected, the Napoleon's Triangle is again equilateral. Surprisingly, there is something else interesting about this situation.

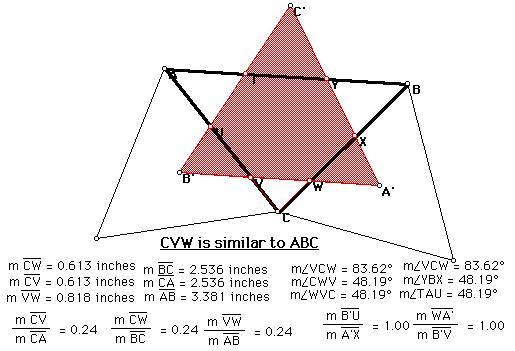
NAPOLEON FIGURE 5

The result is very interesting! Also worth noting is the fact that triangles A'WX and B'UV are congruent.

The final special triangle to look at is a right triangle. Check out right triangle ABC:

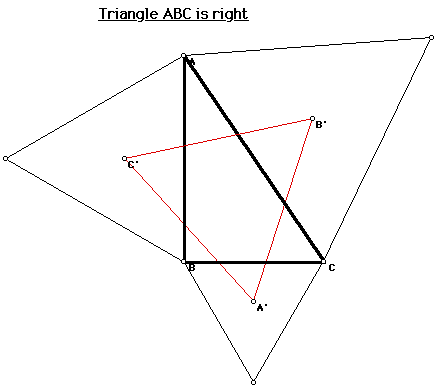
NAPOLEON FIGURE 6

Once again we find an equilateral triangle.

Why are all Napoleon's Triangles equilateral? Is there cases where this is not so? My research on this topic continues, but for now, enjoy the above explorations, and e-mail me with any solutions you may have.