 FIGURE 1
FIGURE 1
Instantaneous rates of change deal with many more topics other than velocity. I have heard it said (perhaps by some former teacher, though I do not recall where) that Archimedes would have given his right arm to have been able to answer such questions (possibly true, since he gave his life to save a few triangles in the sand, though I'm sure they were more than that to him).
Mathematically, how do we deal with this idea of instantaneous rate of change? [If you need to review graphing a line, click calculus internet'slines.] Imagine a function, f(t) which describes a real world situation (such as the distance traveled by your car above) with respect to time. How can we describe the change in f? How can we compare this change to the change in time? What does it mean to do so? Where does this lead us in terms of thinking instantaneously? Newton was the first (my opinion) to give this concept some working legs, though Cauchy later had to slide the foundation underneath Newton's house of calculus.
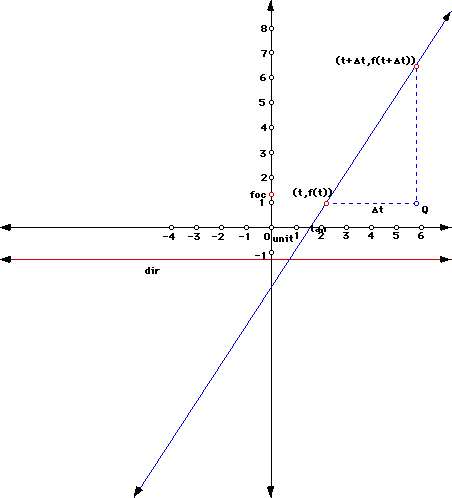
To represent the change in time let us use "delta t" (delta can be denoted with a triangle: this is another story). The corresponding change in f is f(t+delta t) - f(t). See figure 1 below.
 FIGURE 1
FIGURE 1
Here we are thinking of the change in x compared to the change in y or f(t). We begin to see that the rate of change between two points is the same as the slope. From this we can write the expression,
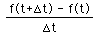 .
.
The average rate of change between two points is thus given by the slope of the secant line. In terms of your car, the secant line is defined by two points which are in coordinates (time, distance [or position]). The slope of this secant is then the average rate of change of your car from one point in time to another. When is it then that we get to instantaneous rate of change? Can you let the change is time approach zero (or be zero)? What would happen to the two points involved? What would happen to the secant line? What would happen to the slope equation we wrote above? To help you think on these questions, click Newton now and explore the environment of the given function.
Did you find any answers? I suppose you have. The slope of the tangent line doesn't exist does it? (according to our formula from figure 1,
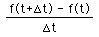 .
.
However, the tan line does have a slope, doesn't it? Newton solved this dilemma by letting the quantity "delta t" be zero as convienent to find such slopes. Many contemporaries protested mightily. How could one let a quantity be zero when it is not actually zero? They could not, however, argue with the results Newton was getting. Later, the definition of limit took care of the paradox, and so we write,
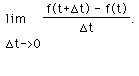
The quantity "delta t" actually gets closer and closer to zero forever, never quite getting there. This is a layman's way to say there is a limit in this situation of zero, and we read the expression above as follows: The limit as delta t approaches zero of the quantity f of t plus delta t minus f of t, all divided by delta t. It is the evaluation of this limit which produces our instantaneous rate of change. This is called taking the derivative of f(t) and is denoted as f'(t) or df/dt. In practice, this is accomplished by letting "delta t" = zero in the expression after some algebraic manipulation or other limit evaluation method. In terms of figure 1, the secant becomes a tangent, "delta t" can get as arbitrarily close to zero as we desire, the two points come together, and the slope of the tangent line can be found. Now, click "Newton" again, run the animation, and think about these things.
(See Limit on the home page for a formal treatment of the concept.)
Let us try to use our animation environment to study some derivatives (instantaneous rates of change) at certain x values. You will need to write the equation of the parabola in the graph by using the provided values of a, h, and k. Recall that the general equation of a parabola can be written as follows:

Using a short rule for evaluating the function for the derivative, you may use y'=2a(x-h) for the derivative equation. Test this formula for the x value at (x+delta x) by dragging the point at x toward the point at (x+delta x) and approximating the limit. Are they the same? Try as many points as you like by dragging the point at (x+delta x) to other spots. Then try a different parabola by moving the focus around. The animation and formulas will work no matter where you place your parabola, even if it opens down. Enjoy! Click "Liebnitz" (to be fair, but that's another story).
Let's finally give credit where credit is due and examine the limit which is the derivative in a spreadsheet environment. Click "Cauchy" to do so.
Let us now look at a function and examine its derivative, as well as its tangent lines. Everything you are looking at was constructed geometrically (I must have some Greek in me). Read the captions carefully and when you look at the graphs, answer the following.
Now go for it! Click A function, its derivative and tangents
For more information on secants becoming tangents click calculus internet's More!
To see secants trying to become a tangent at a non differentiable point click That's a no-no! (Penn State Univ.)
Why did anyone ever believe the world was flat? For the same reason that if you were a mite, you would not be able to distinguish a curve from a tangent on it. For a look, click It's a small, small function of a world.(Penn State Univ.)
For some rules for calculating derivatives, click calculus internet's rules
To return to the homepage click loondog.