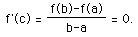
Let us remember for a moment, Rolle's Theorem, which states that on the interval (a< x < b) of some function f(x) where f(a) = f(b), there is some point "c" which has the property that f`(c) is equal to the slope from (a,f(a)) to (b,f(b)) which is zero. That is,
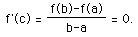
The prerequisites are however that the function must be continuous on the closed interval and that it must be differentiable on the open interval.
For example, consider figure 1 below which is the graph of f(x).
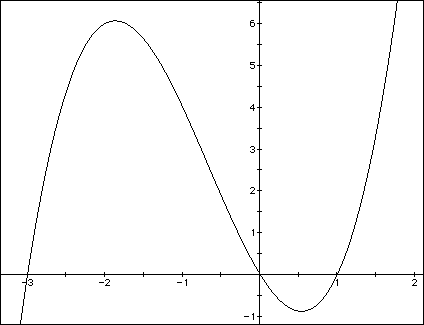
FIGURE 1
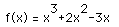
Let us look at the closed interval [-3,1]. Here, we have continuity. There is also differentiability on (-3,1). Also, f(-3) = f(1). The conditions of Rolle's Theorem are thus satisfied. Therefore, there must be at least one place on the interval where there exists a value "c" such that f`(c) = 0.
Recall that f`(c) is the slope of the tangent line to the curve. It is obvious from the graph that there are in fact two such places. (See Figure 2)
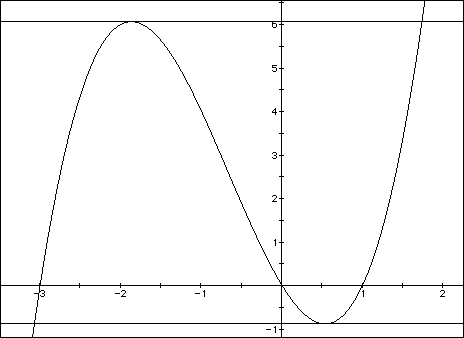
FIGURE 2
The Mean Value Theorem goes further than Rolle's in it analysis of tangent slopes. This theorem states that for a function f(x) which is continuous on some closed interval [a,b] and differentiable on the open interval (a,b), there exists at least one value "c" in the open interval where the derivative of f(x) is equal to the slope between (a, f(a)) and (b, f(b)). That is,
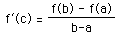 .
.
For example, consider the zoomed in figure below
of our previous function,
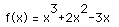 .
.
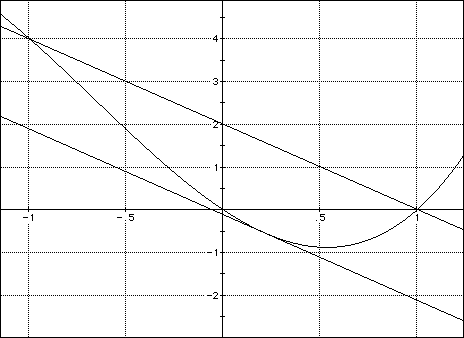
FIGURE 3
Consider the interval [-1,1]. The slope from (-1,4) to (1,0) is
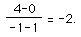
Since f(x) is differentiable on the open interval and continuous on the closed interval, the mean value theorem says there must be at least one value "c" in the interval which gives a tangent line slope of -2. That is, f`(c) = -2. The figure shows the place approximately at x=.215.
One might wonder how to find the equation of this line.
To do so, you need to know the x and y coordinates for the point of tangency of the tangent line with slope -2. First compute the derivative of f,
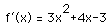 .
.
Setting this derivative (which we know to be the slope of the tangents of f) equal to -2, we obtain x=.215. The y coordinate can be obtained through f by evaluation f(.215) = -.543.
Recall the equation for a line, y=mx + b where m is the slope and b is the y-intercept. We have,
y=-2x + b,
(-.543) = -2(.215) + b,
b=(-.543) + .43,
b=-.113.
Therefore, y=-2x + .113. This is the equation of our tangent line for figure 3.
Let us take another look at the mean value theorem. We will experiment with different intervals of the sine curve. Change the interval by animating. Use the provided tangent line to match the slope from a to b somewhere (perhaps in more than one place) on the curve. Use the "rot" point to change the slope of your tangent. Click mean to experiment. Remember the theorem would not apply without continuity on the closed interval and differentiability on the open one.
For yet another look at the mean value theorem, click mean2. Read the instructions carefully. Experiment with different functions and intervals. Can you find tangent line slopes that match the slope between your interval endpoints?
Try these suggested functions and intervals:
#1)
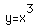 (for various intervals of your choosing)
(for various intervals of your choosing)
#2
y= cosx (for various intervals of your choosing)
#3
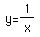 (on the intervals [.2,2] and [-1,1])
(on the intervals [.2,2] and [-1,1])
#4
y=tanx (Try two intervals where the mean value theorem does apply and two where it doesn't.)
For a proof of the mean value theorem, click Rolle Aid now.
Click proof to see something you can use Rolle's Theorem to do.
Click "Pull over son" to see an application of the mean value theorem.
Click loondog to return to the home page.