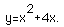
As an example, consider figure A below. This figure shows the graph of
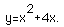
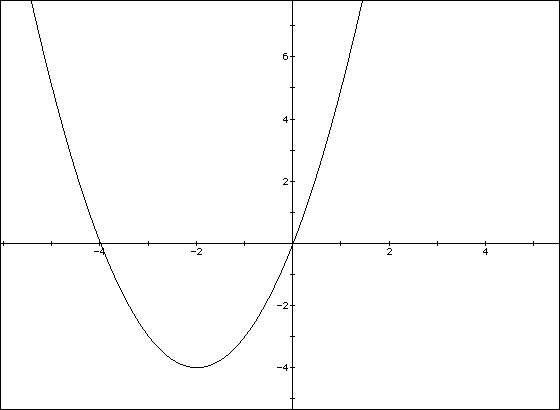
Clearly, a minimizing value exists at the vertex (-2,-4). Figure C shows the graph of f'(x)=2x+4.
Calculus students learn very early that the derivative gives the slope of the tangent line to the curve. What would be the slope of the tangent line at the point on the curve in figure A where the minimum occurs? (at x=-2) See figure B below.
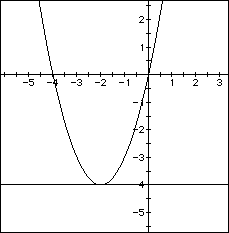
FIGURE B
We can see that the slope of such tangents (at maximums or minimums) would be zero. Algebraically, setting the first derivative equal to zero, note that
2x+4=0
2x=-4
x=-2.
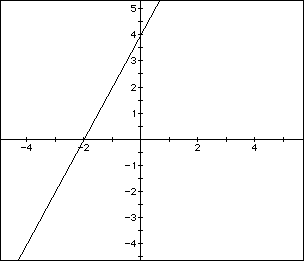
The zero of f'(x) is x = -2. We see that this is also the minimizing value of x in figure A for f(x).
You are an engineer employed by Georgia Kraft Co. Your company is logging old growth timber and producing center (main support) beams for log homes. You must log only a specific number of trees per year according to EPA guidelines. Every tree therefore is important to your company's bottom line, and each one must be cut correctly. It is your job to decide how to set saw mill machinery so that the beams formed are the strongest they can possibly be. You know that the strength varies directly as the beam width and the square of the beam depth. Every type of wood has its own constant. Can calculus tell you this?
The answer is yes, if you can write the equation for the strength and then find a root of its derivative. Let us first examine the problem with the aid of the Geometer's Sketch Pad. Here you will see a graph produced of the strength equation and locate its maximum. Later we will look at the graph of the first derivative and note its root. Click on the word beam to access the sketch. Use the available log sizer, wood constant sizer (you may have to scroll down to get this), and animation feature to determine the strength of some beams.
If you would like to work with a "locus" type construction to explore different wood constants and beam sizes, click locus . As you do, ask yourself how changing the wood constant and the beam size affects the strength of the beam. When you find a width and length that maximizes the strength, find out how (or if) changing the wood constant and beam size affects your solution.
It is clear that the strength does max out. How does calculus find the
maximum strength? As we have seen, it is by finding tangent lines of slope zero
(although undefined slopes and graph endpoints can be important as well). The
original formula for the strength is
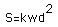 ,
,
where k is the constant for a particular type of wood, w is the width, and d is the depth. k and w can be connected by looking at the log cross section (see below, figure D).
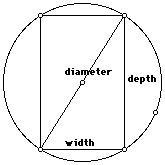
FIGURE D
It can be seen here that the two are related by the pythagorean theorem, (equation 1),
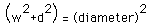 .
.
Therefore, we have (equation 2),

Using this equation to eliminate "d" in the strength equation we have equation 3,
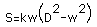 .
(where D = diameter)
.
(where D = diameter)
Also, (simplifying equation 3),
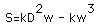 .
.
Taking the derivative, we have equation 4,
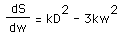 .
.
Setting this equal to zero and solving produces equation 5,
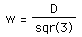 .
.
Of course finding "w" means that the length is determined also. Does this
reasoning agree with the GSP solution you examined previously? Click beam
again to explore some different diameters and obtain the resulting strengths.
Do at least four different diameters. Use the GSP to find the length of "w"
which gives the maximum strength. Then check this against our Calculus solution,
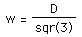 .
.
Let us check an example graphically with the derivative.
Remember that the the value of w above is a root of the graph of the first derivative. Taking the wood constant to be k=1 and the log diameter to be D=4, the graph of the derivative (equation 4) is
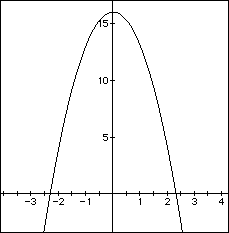
It would appear that the maximizing point should be about w=2.3. Try this in the GSP environment by clicking beam. Then check it with our derived Calculus solution (equation 5). Remember you will have to set k equal to 1 and r=2 (that is, D=4).
Click min to check it out.
Let us look at a max problem in a different environment. However, first you attempt a solution using your knowledge of calculus. Suppose your company wishes to make packaging boxes from 32 inch square pieces of metal. You are requested to design the box with maximum volume by cutting squares out of the corners. 1. What is the equation you will use to maximize? 2. Show how to maximize it using calculus. What size cut do you need to make? (Remember, you are saving the company money!) 3. Explain how your method produced the max. That is, explain your use of the calculus.
Now click box to see the problem in a spreadsheet environment. Investigate cell formulas to see how the values are obtained and why they are labeled as they are. For example, why is dV/dx approximating the derivative? (think slopes!)
Repeat the above problem for a 12 by 12 inch square of metal. Then click box2 for a different visual look at the problem.
To return to the homepage, click loondog.