Essay #1:
"If a brick weighs 3 pounds plus half a brick, how much does a brick and a half weigh"
by
Michelle Lowry and Ashley Little
Answer #1: A brick weighs 3 pounds plus
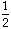 of a brick. Therefore, if x = the weight of the brick then:
of a brick. Therefore, if x = the weight of the brick then:
x = 3 +
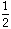 x
x
x -
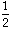 x
= 3
x
= 3
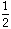 x
= 3
x
= 3
x = 6
So a brick and a half will be 6 +
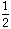 (6)
= 6 + 3 = 9 pounds.
(6)
= 6 + 3 = 9 pounds.
Answer #2: Let x = the amount the brick weighs. If we know that a brick weighs 3 pounds plus half a brick, then half a brick can be calculated as follows:
x = 3 +
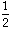 x
x
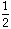 x
=
x
=
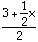
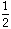 x
=
x
=
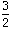 +
+
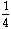 x
x
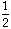 x
-
x
-
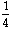 x
=
x
=
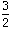
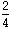 x
-
x
-
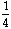 x
=
x
=
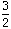
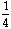 x
=
x
=
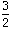
x =
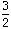 *
*
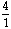
x = 6
Therefore, one brick weighs 6 pounds, thus a brick and a half will weigh 9 pounds.
Answer #3: If one brick weighs 3 pounds plus a half a brick, then two bricks would weigh:
2(3 pounds +
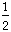 brick)
= 6 pounds + 1 brick.
brick)
= 6 pounds + 1 brick.
This would show one that 2 bricks weigh 6 pounds plus one brick. This means that because they are divided evenly, the other brick would have to weigh 6 pounds. Therefore, a brick and a half would be 6 pounds plus 3 pounds which is a total of 9 pounds.
Answer #4: If one brick weighs 3 pounds plus half a brick, then we should be able to find what a brick and a half weighs by the following:
Let us say that weight of the brick = b.
Then, a brick and a half is b +
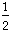 b
= 3 +
b
= 3 +
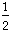 b
+
b
+
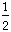 b
b
b +
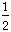 b
= 3 + b
b
= 3 + b
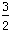 b
= 3 + b
b
= 3 + b
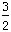 b
- b = 3
b
- b = 3
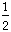 b
= 3
b
= 3
b = 3 * 2
b = 6
Therefore a brick and a half will weigh 6 pounds + 3 pounds, or 9 pounds.
Answer #5: Another way to examine the problem is to create a spreadsheet. By examining various weights, various half weights, and the difference of three pounds one can see if other answers are feasible.
If the brick half of the brick subtracting the 3
weighs: would weigh: given pounds:
1 0.5 -2.5
1.5 0.75 -2.25
2 1 -2
2.5 1.25 -1.75
3 1.5 -1.5
3.5 1.75 -1.25
4 2 -1
4.5 2.25 -0.75
5 2.5 -0.5
5.5 2.75 -0.25
6 3 0
6.5 3.25 0.25
7 3.5 0.5
7.5 3.75 0.75
8 4 1
8.5 4.25 1.25
9 4.5 1.5
9.5 4.75 1.75
10 5 2
10.5 5.25 2.25
11 5.5 2.5
11.5 5.75 2.75
12 6 3
12.5 6.25 3.25
13 6.5 3.5
13.5 6.75 3.75
By examining the chart, one can see a few of the infinite amount of weights possibile if we knew the weight of the entire brick was half of the weight of the brick only (See the second column). However, the third column shows us what happens when we remove the three known pounds that are contained in the brick. Having a brick that weighs less than six pounds makes no sense because of a negative difference in weight. Furthermore, the difference would have to be zero because half of the weight has been taken out, leaving only the three pounds. Three pounds minus three pounds will result in zero if it is the brick we are considering. This only happens when the brick weighs six pounds as shown in the table. Therefore, if one brick weighs 6 pounds, then a brick and a half will weigh 9 pounds.
Answer #6: We know a brick weighs 3 pounds plus half a brick. If we multiply that brick by 3, to see what 3 bricks will weigh we get:
3(3 pounds +
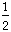 brick)
brick)
= 9 pounds +
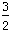 brick
brick
= 9 pounds +
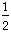 brick
+ 1 brick
brick
+ 1 brick
= 6 pounds + 3 pounds +
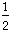 brick
+ 1 brick
brick
+ 1 brick
= 6 pounds + 1 brick + 1 brick
= 6 pounds + 2 bricks
Therefore, 3 bricks = 6 pounds + 2 bricks so a brick weighs 6 pounds which means a brick and a half weighs 9 pounds.