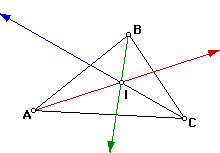
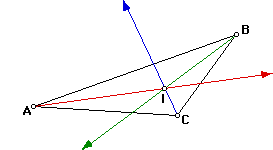
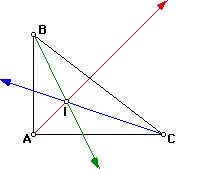



As you can see for an given triangle, whether it be acute, obtuse, or
right, the incenter is always inside the given triangle.
Orthocenter: The lines that contain the altitudes of a triangle intersect
in one point. The point of concurrency of the altitudes is called the orthocenter.
First we will construct the altitudes, which is the perpendicular line from
the vertex to the oppsite side of the given triangle. The point O at which
they meet is the orthocenter.
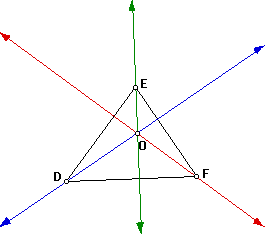
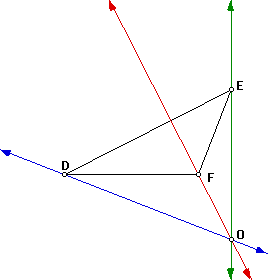
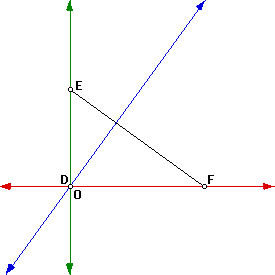
As you see in each of the given triangles the orthocenter is in a different
location. In the acute triangle the orthocenter is inside the triangle.
The obtuse triangle has the orthocenter outside of the triangle. The right
triangle has the orthocenter at the same point as the vertex of the right
angle. Therefore in the right triangle D=O.
Circumcenter: The perpendicular bisectors of the sides of a triangle
intersect in a point that is equidistant from the vertices of the triangle.
The point of concurrency of the perpendicular bisectors of the sides of
a triangle is called the circumcenter. First we will constuct the
perpendicular bisectors, which are the perpendicular lines to each side
at the midpoint of the given side. The point C at which the perpendicular
bisectors meet is the circumcenter.
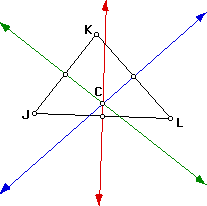
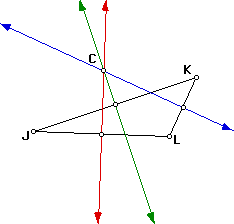
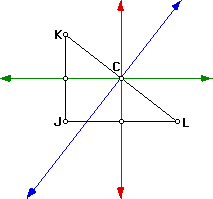
As you can see in each triangle the circumcenter is in a different location.
In the acute triangle the circumcenter is inside the triangle. The obtuse
triangle has the circumcenter outside the triangle. The right triangle has
the circumcenter on the hypotenuse of the triangle.
Centroid: The medians of a triangle are concurrent. The length of
the segment of a median from the vertex to the point of concurrency is 2/3
the length of the entire median. The point of concurrency of the medians
of any triangle is called the centroid. First we will construct the
medians of the triangle and the point C' at which they meet is the centroid.
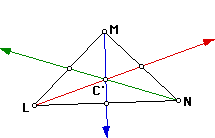
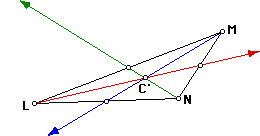
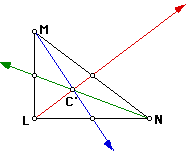
As you see in each given triangle the centroid is always inside the triangle.
Though it is not the same as the incenter it is still a point inside the
given triangle.
The constructions presented thus far can be used in performing constructions
involving circles and their related lines, rays, and segments.
Now we will use circles to make other constructions using these lines, rays,
and segments. Eventually we will inscribe and circumscribe a circle in a
triangle.
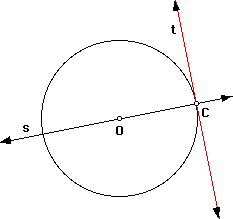
Construct a tangent to a circle at a point on the circle.
Given point C on circle O. We want a line tangent to circle O. We will first
draw the circle with center O and point C on the circle. Then draw a line,
s, through point O and C. Draw a line, t, perpendicular to line s through
point C. This will be the line tangent to circle O.
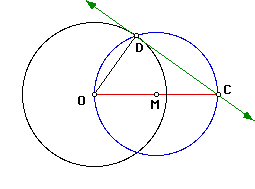
Now we will construct a tangent to a circle through a point in the exterior
of the circle. Given point C in the exterior of circle O. We want a line
tangent to circle O. We will first draw the circle with center O and a point
C outside the circle. Then draw a segment between point O and C. Construct
the midpoint M of segment OC. With M as the center and with the segment
MO as the radius, draw the circle M intersecting circle O at point D. Then
with segment OD make a perpendicular line DP to this segment at point D.
Therefore line DP is tangent to circle O.
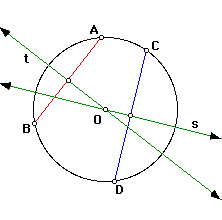
Now we will locate the center of a given circle. Given the circle O with
unknown locaton of center O. First we will draw any two nonparallel chords
segment AB and segment CD. Then we will construct lines t and s, the perpendicular
bisectors of segment AB and segment CD, respectively. The point at which
these two lines intersect is the center of the circle, O.
All of the constructions lead up to circumscribing and inscribing circles
about a given triangle.
Now we are going to circumscribe a circle about a given triangle. Given
triangle ABC. We want to circumscribed circle D about triangle ABC. First
we will construct perpendicular bisectors of any two sides of triangle ABC,
intersecting at D, which is the circumcenter of the given triangle. With
center D, draw a circle D with radius DA. Therefore circle D, which passes
through points A, B, and C, will circumscribe the triangle ABC.
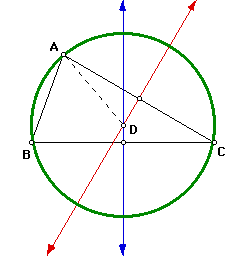
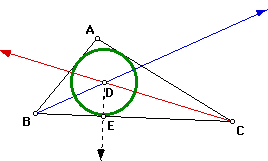
Now we are going to inscribe a circle about a given triangle. Given triangle
ABC. We want to inscribe circle D about triangle ABC. First we will construct
the angle bisectors of any two angles of triangle ABC, intersecting at point
D, which is the incenter of the given triangle. Now construct the perpendicular
from point D to any side of triangle ABC. This intersection is point E.
Then to construct the inscribed circle use center D and radius segment DE.
Therefore circle D is inscribed in triangle ABC.
All of these constructions intertwine. You have to be able to do the
basic constructions in order to continue with constructions like inscribing
and circumscribing figures. With these basic constructions you can continue
with inscribing or circumscribing other figures. Now you can determine if
there is any change, when you have a given triangle that is acute, obtuse,
or right, in where or what the circle looks like, when inscribing or circumscribing
a circle. Then try other objects and determine if there are any similarities
or differences.