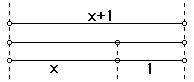
The ratio, called the Golden Ratio, is the ratio of the length
to the width of what is said to be one of the most aesthetically
pleasing rectangular shapes. This rectangle, called the Golden
Rectangle, appears in nature and is used by humans in both art
and architecture. The Golden Ratio can be noticed in the way trees
grow, in the proportions of both human and animal bodies, and
in the frequency of rabbit births. The ratio is close to 1.618.
Whoever first discovered these intriguing manifestations of geometry
in nature must have been very excited about the discovery.
A study of the Golden Ratio provides an intereting setting for
enrichement activities for older students. Ideas involved are:
ratio, similarity, sequences, constructions, and other concepts
of algebra and goemetry.
Finding the Golden Ratio. Consider a line segment of a length
x+1 such that the ratio of the whole line segment x+1 to the longer
segment x is the same as the ratio of the line segment, x, to
the shorter segment, 1.
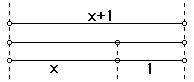
Thus,
The resulting quadratic equation is
A positive root of this equation is
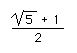 ,
,or 1.61803... This irrational number, or its reciprocal
is known as the Golden Ratio, phi .
Now we will construct the Golden Rectangle. First we will construct
a square ABCD.
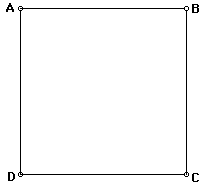
Now we will construct the midpoint E of DC.
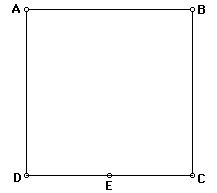
Extend DC. With center E and radius EB, draw an arc crossing
EC extended at C.
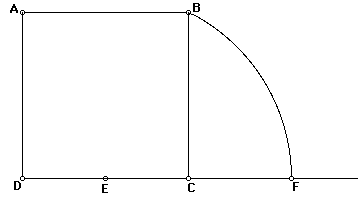
Construct a perpendicular to DF at F.
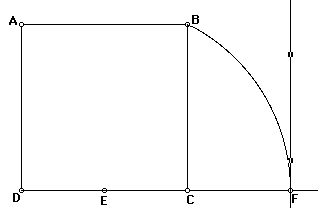
Extend AB to intersect the perpendicular at G.

AGFD is a Golden Rectangle.
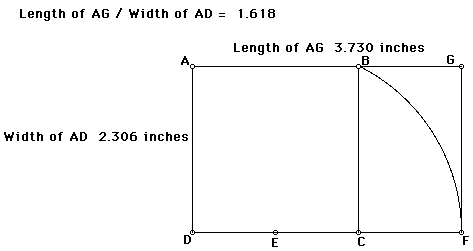
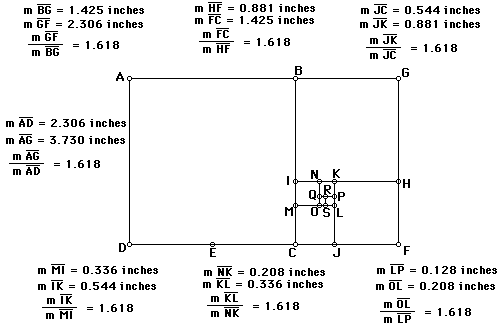
Now we will measure the length and width of the rectangle. Then
we will find the ratio of the length to the width. This should
be close to the Golden Ratio (approximately 1.618).
Now we will take our Golden Rectangle and continue to divide
it into other Golden Rectangles.
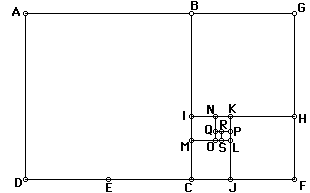
Within this one large Golden Rectangle there are six other
Golden Rectangles.
When you measure each Golden Rectangles length and width you will
see that the ratio of the length to the width is the Golden Ratio
(spproximately 1.618).
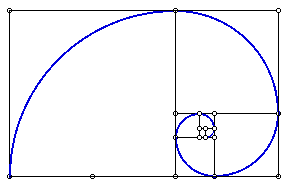
Now we will construct the spiral through the whole Golden Rectangle.
Return to Leanne's homepage.