---

EULER LINE

by Derelle McFarland

---

The Euler line is the line on which the Orthocenter H, Centroid G, Circumcenter C and Nine Point Center F lie. The Incenter I lies on the Euler line if the triangle is isoceles.

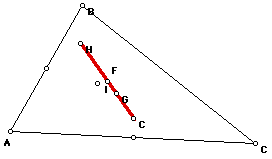
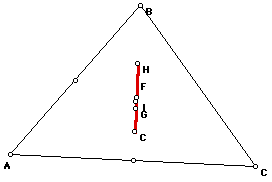
Now I will prove why these points are colinear.
By constructing the altitude from vertex C to line AB we get a line that goes through point H, the orthocenter. By constructing the perpendicular bisector of line AB we get a line that goes through point C, the circumcenter. Line r is parallel to line v because they are both perpendicular to line AB. So line CH is a transversal through lines v and r. Therefore point C and point H are colinear.

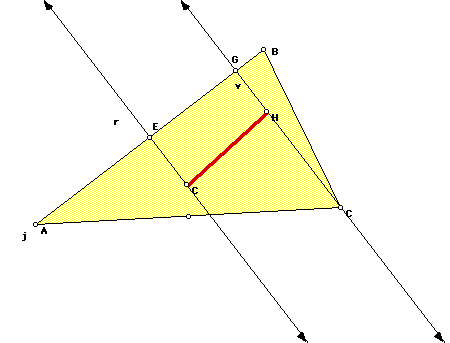
Now I will construct a line s parallel to r and v through point G. Since s and r are parallel the Euler line is a transversal. Thus point G and point H are colinear. Since s and v are parallel the Euler line is a transversal. Thus point G and point C are colinear. Therefore points C, G and H are colinear.

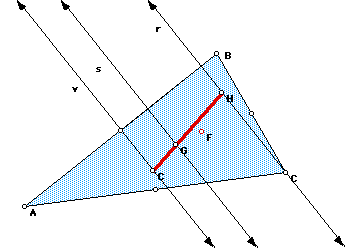
The distance from the circumcenter, C, to the centroid, G, is always a third of the length of the Euler line. The distance from the orthocenter, H, to the centroid, G, is always two thirds of the length of the Euler line. Click here for demonstration.

---

I will now construct a triangle inside triangle ABC from the midpoints of the sides. Then I will construct the Euler line of the new triangle. Notice that the new Euelr line is half the length of the original Euler line for any triangle. Click here to see the ratio.

---

Back to Derelle's home page