
CONSTRUCTION PORTFOLIO
by Derelle McFarland
Objectives
*To use compass and straight edge to make constructions
*To use GSP to make constructions
*To use the properties of polygons
*To construct a portfolio containing your constructions
Day
1
On the board I will have listed the following figures, equilateral triangle,
obtuse triangle, isoceles triangle, rhombus, trapezoid, isoceles trapezoid,
kite, parallelogram, rectangle, square, and circle.
As a class we will brainstorm the properties of these figures. The students
should remember the characteristics from middle school, but if they don't
they are in their geometry book. When we finish discussing, and the students
have taken notes on these I will explain the next two weeks assignment.
They are to create a portfolio of the constructions we will be constructing
for the next two weeks. Some days we will use GSP and others we will use
compass and straight edge. Their portfolio will be worth a test grade and
will be broken into presentation (15pts), organization (15pts), disc (15
pts), reflection (20pts) and contents (35pts). Today and tomorrow they will
construct the figures we discussed using compass and straight edge. I will
allow them to work in groups but they must do their own construction. For
homework each night they are to describe any observations they made about
their constructions, difficulties they had or things they enjoyed to be
their reflections included in their portfolio.
Day 2
Continue constructions using compass and straight edge.
Day
3
Today we will go to the computer lab to do our constructions using GSP.
I will give each student a disc for their use. I will explain that the disc
must be organized and turned in for 15 points of the portfolio grade. The
students have used GSP briefly before. I expect lots of questions so I will
refresh their memory of using GSP. I will go over the icons on the left
bar on the computer which projects onto the screen, but I will require the
students follow along on their computer. I will explain the proper GSP construction
that does not "move" and the improper ones that don't "stick".
There are exactly enough computers for each student to have their own. Once
we have reviewed the use of GSP, I will allow them to begin constructing
the same constructions from our discussion on Monday. Each student will
have a disc to use that I will keep at the end of the day. This will ensure
that students who have the technology at home are staying on task in class.
Day
4
Continue constructions using Geometers Sketch Pad.
Day 5
Today we will construct inscribed figures. There will be eight constructions
to be done on both GSP and compass and straight edge. We will go to the
lab to do the GSP part and the compass and straight edge part will be homework.
The eight constructions are:
1) square inscribed in a triangle
2) circle inscribed in a triangle
3) triangle inscribed in a triangle
4) square inscribed in a square
5) circle inscribed in a square
6) triangle inscribed in a square
7) triangle inscribed in a circle
8) square inscribed in a circle
Day 6
Today I am going to teach the students how to construct the altitude, medians,
angle bisectors and perpendicular bisectors of a triangle to find the orthocenter,
centroid, incenter and circumcenter of a triangle. I will bring the computer
into my room and show my work on the overhead screen. I will allow students
to come up and help with the constructions. Here is what I will show.
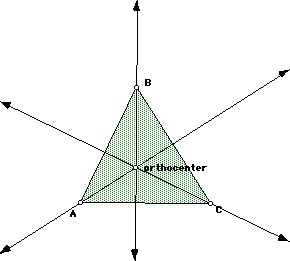
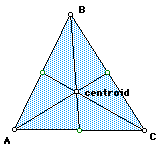
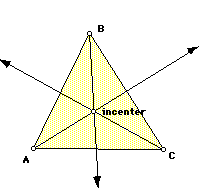
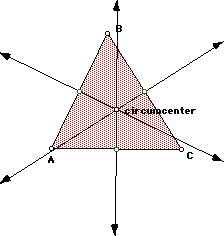
This should take most of the period, so I will allow them the end of the
period to begin their compass and straiht edge construction of these points
for equilateral, isoceles and obtuse triangles. They are to reflect upon
the different postitions of these points depending on the type of triangle.
Day
7
Today they will construct the orthocenter, centorid, incenter and circumcenter
for an equilateral, isoceles and obtuse triangle in the lab using GSP.
Day
8
We will be in the lab again today. We will use the previous lessons to construct
the nine point circle, eight point circle, Euler line and Pedal triangle.
After I demonstrate how to construct the nine point circle (and they follow
along on their computer), I will give the students the following ditto describing
the characteristics of each, and allow them to explore them on GSP.
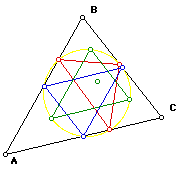
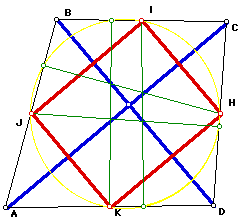
Eight point circle: Let ABCD be a quadrilateral with perpendicular diagonals.
The midpoints of the sides determine a parallelogram with sides parallel
to the diagonals. The eight point circle passes through the four midpoints
and the four feet of hte perpendiculars from the opposite sides.
Euler Line: The euler line is the line on which the orthocenter, centroid,
circumcenter and nine point center lie. Investigate what kind of triangle
has a Euler line that also contains the incenter. Be sure to write about
this in your reflections.

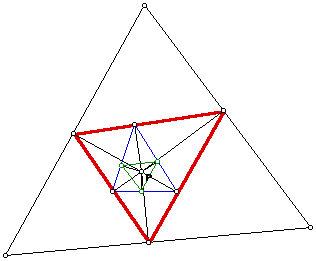
Pedal Triangle: Given a point P, the pedal triangle of P is the triangle
whose vertices are the feet of the perpendiculars from P to the sides. What
do you think the second and third pedal triangles would be like. Investigate
and explain in your reflection for today.
Day 9
Today we will be in the lab to allow students to complete any unfinished
constructions. They should have all of their constructions on paper for
their portfolio, but their disc should also be neatly organized so that I
can be sure that their GSP constructions "stick".
Day
10
Today is the last day of the unit. The students will break into groups of
5 and share their portfolios. As they leave class they are to turn in their
portfolios.
Back to Derelle's
home page









