Lori Pearman

Essay #1

Minimization of the Surface Area of a Cylinder
with a given Volume

This essay will investigate ways to find the minimum surface area of a cylinder if the volume is fixed. I will first look at a specific example, and then I will generalize the results for other cases.

Suppose a company wants to design and manufacture soup cans of a given volume. The volume of each can is to be 850 ml. To minimize costs, the company wishes to design a can that requires the smallest amount of material possible. How can we find the best dimensions for the can?

The volume of a cylinder is V = [[pi]](r^2)h, where r is the radius and h is the height. The surface area S = 2([[pi]] r^2) + h (2[[pi]] r). The first part of the equation is due to the fact that the top and bottom of a cylinder are circular disks, and the area of a circle is [[pi]]r^2. The second part of the equation is the lateral surface area of the cylinder which is equivalent to a rectangle with an area that is h*2[[pi]]r. This can be shown by unfolding a cylinder by separating the top and bottom except at one point, and rolling out the lateral surface. (See the below picture.)

To investigate this problem, I went to the Geometer's Sketch Pad and constructed a cylinder. I made a segment for radius and one for height. One could drag either segment to change the radius and height respectively. Then I calculated the area and circumference of one of the circles. From these, I also calculated volume and surface area of the cylinder. Below is the cylinder I constructed.

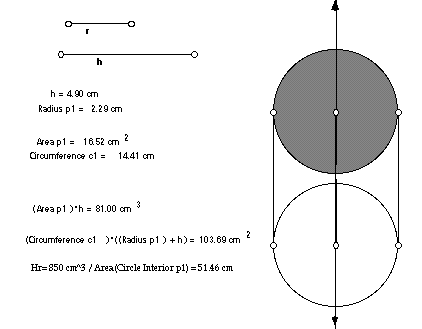
P1 is the label of the shaded circle interior, and C1 is the circle itself. [(Area p1)*h] is the volume of the cylinder, and [(Circumference c1)*((Radius p1)+h)] is the surface area of the cylinder. The equation for Hr above gives the height that (with the shown radius r) would produce a volume of 850 ml.

Now let's take a look at a spread sheet chart of different radius values and their corresponding heights (heights which will give a volume of 850 ml). Let's also see what the corresponding surface area is for different radii.


Radius (cm)      Height (cm)       Surface Area    
     0.50          1082.25           3401.57       
     0.75           481.00           2270.20       
     1.00           270.56           1706.28       
     1.25           173.16           1369.82       
     1.50           120.25           1147.47       
     1.75            88.35            990.67       
     2.00            67.64            875.13       
     2.25            53.44            787.36       
     2.50            43.29            719.27       
     2.75            35.78            665.70       
     3.00            30.06            623.22       
     3.25            25.62            589.44       
     3.50            22.09            562.68       
     3.75            19.24            541.69       
     4.00            16.91            525.53       
     4.25            14.98            513.49       
     4.50            13.36            505.01       
     4.75            11.99            499.66       
     5.00            10.82            497.08       
     5.25             9.82            496.99       
     5.50             8.94            499.16       
     5.75             8.18            503.39       
     6.00             7.52            509.53       
     6.25             6.93            517.44       
     6.50             6.40            527.00       
     6.75             5.94            538.13       
     7.00             5.52            550.73       
     7.25             5.15            564.74       
     7.50             4.81            580.10       
     7.75             4.50            596.74       
     8.00             4.23            614.62       
     8.25             3.98            633.71       
     8.50             3.74            653.96       
     8.75             3.53            675.34       
     9.00             3.34            697.83       
     9.25             3.16            721.39       
     9.50             3.00            746.00       
     9.75             2.85            771.65       
    10.00             2.71            798.32
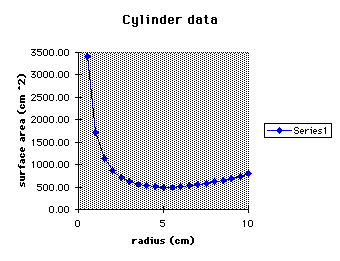
The smallest surface area in the chart is 497.08, which occurs when the radius is 5 ( and height is 10.82) cm.

Now let's plot radius versus surface area on a spread sheet graph to get an idea of which radii give the smallest surface areas.

Below is a graph from Algebra Xpresser showing radius versus surface area. Notice that the surface area is smallest when the radius is approximately 5. (And when r =5, height is approximately 10.)

One way to check our previous estimations is by using calculus. As stated earlier, S=2[[pi]]r(h+r) and h=850/([[pi]] r^ 2). To get S in terms of one variable, we can plug (850/[[pi]]r^2) in for h in the equation. We then get S = 2[[pi]]r((850[[pi]]r^2)+r) = 1700/r + 2[[pi]]r^2. Taking the derivative of S, we get S' = -1700r^2 + 4[[pi]]r. Setting this equal to zero and solving for r, we get that r is approximately 5.13 cm. This gives us our desired volume with a minimum surface area of 496.7 cm^2. (Height is 10.28 cm.) Thus, to minimize surface area, the height of the can must be the same as the diameter of the ends (h = 2r).

The relationship h = 2r will hold to minimize the surface area for any fixed volume.

Below is a proof of this which used the arithmetic mean- geometric mean inequality which states that for positive A1, A2, . . ., An,

(A1+ A2+. . .+An)/n > or = (A1*A2*. . .*An)(1/n) , with equality iff A1=A2= . . . =An.

Proof: As stated earlier in the essay, V = [[pi]]r2h implies h = V/([[pi]]r2),

and 

           S = 2[[pi]]r2 + 2[[pi]]rh


              = 2[[pi]]r2 + 2[[pi]]r[V/([[pi]]r2)]


              = 2[[pi]]r2 + 2V/r


              = 2[[pi]]r2 + V/r + V/r .
By the arithmetic mean- geometric mean inequality, S > or = [(2[[pi]]r2)(V/r)(V/r)](1/3) = (2[[pi]]V2)(1/3), which is a constant. Thus, S is larger than or equal to this constant. Since we want to minimize S, we want it to equal the constant. This happens iff 2[[pi]]r2 = V/r, which leads to h = 2r.

Thus, several approaches can be taken to solve this minimization problem. We can get an estimation for the answer or find a relationship between r and h that will give the minimum volume. Algebra, geometry, and calculus can be used.
Return to Lori's EMT 669 Page