by Cathy Perkins
The following problem was a problem presented to me in the Spring of 1994 in the EMT 525 Problem Solving course. I didn't solve the problem then, so I thought I would attempt it again.
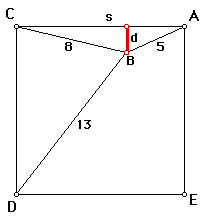
Problem: Four roads form a square ACDE with side length s. A barn B is 5 miles from A, 8 miles from C, and 13 miles from D. What is the shortest distance from the barn to the nearest road?

The shortest distance from the barn to the nearest road would be the perpendicular distance of the segment from the barn B to road AC, indicated in red and labeled d in the figure above. To find this distance, I first will need to find some of the angle measures. Specifically, I want to find the measure of angle CAB.
To attempt to find some of the angle measures, I began by rotating triangle ABC about C 270 degrees until A and D coincide. I labeled the image of B, B'. I connected Band B'. The following sketch shows the transformation.
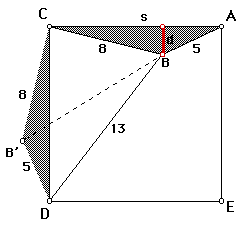
Angle BCB' is a right angle, and since CB'=CB, Triangle BCB' is an isosceles right triangle. Using the Pythagorean Theorem, we see that
= 8*sqrt(2)
Using the Law of Cosines, c^2 = a^2 + b^2 - 2abcosx, we can find the measure of angle BB'D.
25 = 128 + 169 -294.156421cosx
-272 = -294.156421cosx
cosx = .924678
x = 22.4 degrees
We can also find the measure of angle BB'D this way.
169 = 128 + 25 - 113.137085cosx
169 = 153 - 113.137085cosx
16 = -113.137085cosx
cosx = -.14142
x = 98.1 degrees
We can add these measurements to our figure.
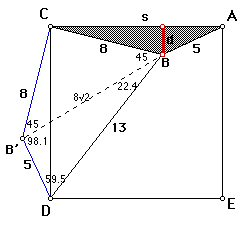
The measure of angle CB'D = the measure of angle CBA = 45 + 98.1 = 143.1
To find the length of s, again I used the Law of Cosines.
s^2 = 64 +25 - 80(-.79968)
s^2 = 99 + 63.97477
s^2 = 162.97477
s = 12.766 miles
Now that I know s, I can once again use the Law of Cosines to find the measure of angle CDB.
64 = 169 + 162.97477 -331.916cosx
-267.970756 = -331.916cosx
cosx = .807345
x = 36.16 degrees
B'DC + CDB = B'DB = 59.5, so B'DC + 36.16 = 59.5. Therefore, B'DC = 23.34. B'DC = CAB = 23.34 degrees. Our figure now looks like this:
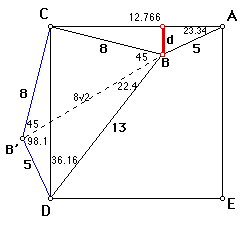
We can find the distance from the barn to road AC now by using ratios of right triangles. We have the following right triangle:
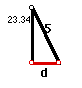
.3961866 = d / 5
d = 5*.3961866
d = 1.98 miles
From the previous calculations, I found that the shortest distance from the barn to the nearest road is 1.98 miles.