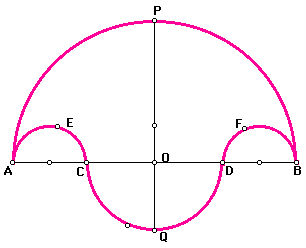
The Alexandrian mathematician Archimedes ( 287 - 212 BC) wrote the Book of Lemmas, which was a collection of 13 geometrical propositions. In the book, Archimedes introduced the figure known as the "salt cellar" or "salinon". The construction of the figure goes as follows:

1. Construct a segment AB.

2. On the diameter AB, construct a semicircle.

3. Construct segments AC = DB on the diameter AB.

4. With AC and DB as diameters, construct semicircles, on the same side of semicircle AB.

5. With CD as the diameter, construct a semicircle on the other side of AB.

The GSP construction of the figure follows:

The region outlined in pink is the "salt cellar." In this figure, segment PQ is the line of symmetry of the figure. Let's construct a circle with PQ as the diameter. The GSP construction follows:

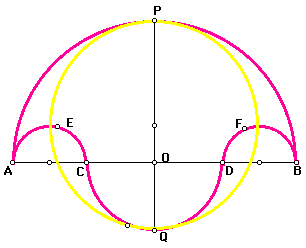
It appears that the circle with PQ as its diameter has the same area as the salt cellar. Is this always the case? We can use GSP and notice the areas as we change length of the diameter AC, and therefore change the area of the salt cellar. Click