The problem that I am referring to is one of the three construction problems of antiquity that Plato supposedly insisted be performed with a collapsible compass and unmarked straightedge. The 3 problems are as follows:
** Construct a square whose area is equal to the area of a given circle.
(Squaring of the Circle, Quadrature of the Circle)
** Find the edge of a cube having a volume twice that of a given cube.
** Trisect a arbitrary angle.
The problem that the Braves have "solved" is the trisection of an arbitrary angle.
Actually, the problem has not been solved because the solution was accomplished mechanically, not according to Plato's rules. Pierre Wantzel (1814 - 1848) proved the impossibility of trisecting any given angle by Plato's restrictions.
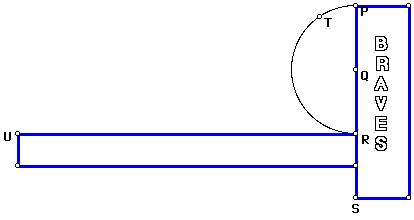
The method of "solving" the trisection problem is to construct a TOMAHAWK (here is where the Braves come in). To construct the tomahawk, construct PQ = QR = RS with PTR a semicircle on PR as diameter. Construct UR perpendicular to PS. Additional segments are added to complete the tomahawk. The GSP construction follows:
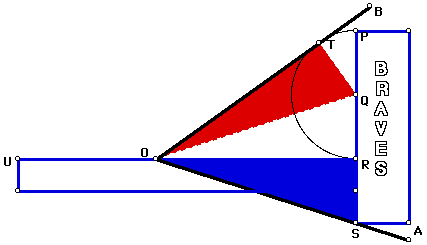
Once we have our tomahawk constructed, we can trisect an arbitrary angle. To do this we can place our angle AOB on the tomahawk so that the point S on our tomahawk lies on OA, the line segment UR passes through O, and the semicircle PTR is tangent to OB at T. The GSP construction of trisecting an angle follows:
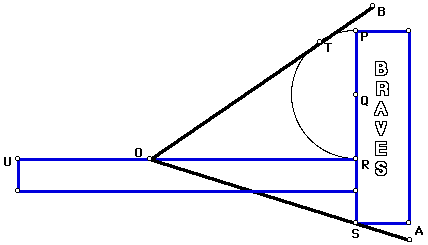
We see here that angle AOB has been trisected by the tomahawk; the measure of angle ROA is one-third the measure of angle AOB. We can show this trisection for various other angles by animating the point T along the semicircle PTR. Click here to open the GSP demonstration.
We need to prove that this construction will trisect the angle. To do this we will prove that we have 3 congruent triangles and therefore 3 congruent corresponding angles.
First let's construct the triangles OTQ and OQR by constructing segments OQ and QT.
PROOF:
* QT = QR since they are both radii of the semicircle PTR.
* QR = RS by construction, Therefore QT = QR = RS.
* OQ = OQ.
* Angle ORQ is a right angle by construction and angle OTQ is a right angle since the tangent OB is perpendicular to the radius QT.
* The measure of angle ORQ = the measure of angle OTQ since all right angles are congruent.
* Triangle OTQ is congruent to triangle ORQ by Side-Angle-Side.
* OR = OR
* Angle ORS is a right angle by construction.
* The measure of angle ORQ = the measure of angle ORS since all right angles are congruent.
* Triangle ORQ is congruent to triangle ORS by Side-Angle-Side.
* By transitivity, triangle OTQ, triangle ORQ, and triangle ORS are all congruent.
* Corresponding parts of congruent triangles are congruent, so angles TOQ, ROQ, and ROS are all congruent.
* < AOB = < TOQ + < ROQ + < ROS, so angle ROS is one- third of angle AOB.