This essay is a series of Geometer's Sketchpad animations where a point P is animated about an equilateral triangle and a square. An envelope of circles is traced where P is the center of each circle and each circle passes through a fixed point S. The point S is moved in many different places on the polygons to achieve different effects. Included in the essay are several opportunities for you to go to a Geometer's Sketchpad file and explore with the created polygons.

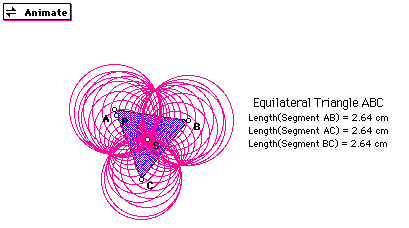
We began with the simplest regular polygon an equilateral triangle. Click here to animate. It was constructed in GSP and a point P was created on it. Then using a script I created the point S and made it the incenter, orthocenter, etc. of the equilateral triangle. Using the animation as P goes around the equilateral triangle ABC the following picture is produced. (This is only a picture the animation will not work)

The envelope of curves produced is three circles with equal areas and the centers being the vertices of the triangles. We know this because of the way they were created. The radius of all the circles is the same because the point S was created to be equidistant from the vertices on the triangle. When the point S is moved inside the equilateral triangle you always get an envelope of three circle with areas that vary according to where S is placed. From the overlap of the circles we see a three leaf rose.

Next we let S be the midpoint of one of the sides on the triangle.

Below is the picture produced by the animation.

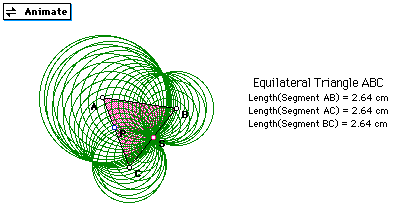
This produces a beautiful set of Mickey Mouse ears. Again we have three circles with the vertices as the centers, two have equal areas and the third appears to be twice the area of the other two. When the point S is place on the triangle not at the midpoint of a side, produced is three circles one with a considerably smaller area that the other two. If the point S is one of the vertices of the triangle then only two circles show on the screen and they have equal area because the radius of the two are the same. From the vertex with that S is closest to.

Next we moved S to the outside of the triangle, this still produced three distinct circles. If S lies on the line of the vertices then it appears that only two circles are created. If you actually look at the animation, three circles are being created, but the third circle is enclosed in the two you see on the screen. Below is a picture of the envelop of circles.

No matter where S is located inside, outside, or on the circle, the vertices of the triangle are the centers of the circles.

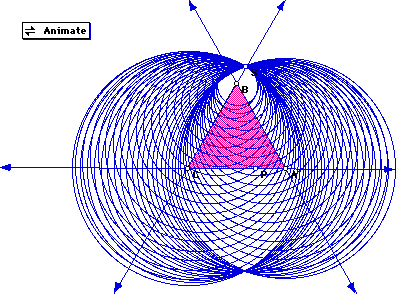
The second set of explorations were done moving the point about a square and varying the location of point S. This link to GSP can be used to explore the curves. Click here to animate. First we let S be the midpoint on one side of the triangle. Four circles are created, two pair that are congruent. The vertices of the square are the centers of the triangles. Below is a picture of what is created.

When S is on the square but not at the midpoint of a side four circles are still created, but they do not have equal areas. The vertices of the square are still the centers of the circles. If S is on one of the vertices we only create three circle, two of which have equal areas. Once again this curve appears to be a nice set of Mickey Mouse ears. When S is at the center of the square you get exactly what you would expect four congruent circles, with the vertices as the centers.

Inside the circles we can see a four leaf rose, on the triangle we saw three leaf rose formed from the overlap of the circles. If S is placed in the circle not at the center four circles are formed, with the vertices as the centers, not having equal areas.

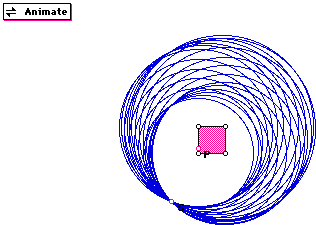
The curves formed by the circles get much more interesting as S moves outside the square. Below is a picture with S outside the circle. As S moves farther away from the circle the curve formed by the envelop of circles appears to look more and more like a limacon.

We have only explored a few of the polygonal paths. This could be extended to include all other regular polygons or any polygon. The envelop of curves formed from each of the polygons can be an extensive search.