INSTRUCTIONAL UNIT 1
By Craig Rimpley
THREE DIMENSIONAL SOLIDS, VOLUME AND SURFACE AREA:
This is an introduction to three dimensional objects and the mathematical
connections that can be explored within this subject. First we need to understand
the differences between surfaces and solids. Both surfaces and solids are
considered to be three dimensional figures but there are some specific differences.
DEFINITIONS:
A SURFACE IS THE BOUNDARY OF A THREE DIMENSIONAL OBJECT.
Example: a beach ball is a surface.
A SOLID IS THE UNION OF THE BOUNDARY OF AN OBJECT WITH THE SPACE
OR REGION CONTAINED BY THE BOUNDARY.
Example: a bowling ball is a solid.
Both the bowling ball and beach ball have surfaces. We can see the
differences between these two types of objects by looking at the space within
each surface. The beach ball is filled with air that can be removed and
replaced with ease. The bowling ball surface is filled with bowling ball
all the way through, hence the name solid.
The shapes we will work with over the next few days are cylinders. We have
done investigations with rectangles and squares. The infamous "box
problem" was the last project or problem presented. So our students
have some general knowledge of volume that should have been acquired duing
this exercise.
We can start to explain surface by going back to the "box problem".
The students can grasp an understanding of surface area by moving backwards
in the "box problem". If we open our box up into the flat piece
of paper we are looking at the surface area of our box. Once we have made
this connection between a three dimensional object and surface area we are
ready to explore a similar problem.
"THE CYLINDER PROBLEM"
Given a standard piece of paper make cuts so that you can fold the paper
into a cylinder. The piece of paper should look like the following:
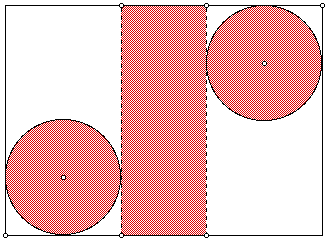
Once the students have completed their cylinders they need to compare
with each other and ask the questions: Which of the cylinders that were
made in class today has the largest volume and surface area and which has
the smallest. If the construction of a cylinder is to time consuming to
be part of the class then the instructor can bring prepared examples of
each step of the construction and quickly present this to the class. The
construction of the box needs to be part of the preparation of this lesson,
so the students have a physical understanding of what was done.
Now we have two problems that are very similar mathematically, but visually
different. If we compare and investigate each problem our students should
be able to realize the likeness and differences between the two.
Most geometry textbooks are kind enough to give us the formulas for
surface area and volume of a right cylinder. The text I referenced broke
surface area into :
LATERAL AREA
The lateral area of a right cylinder is the product of its height
and the perimeter of its base.
BASE AREA
This is simply the area of the circle that is the base of our
right cylinder or PI*RADIUS^2.
The formula for volume of a right cylinder is the product of its height
and the area of its base. We can use these formulas to explain the differences
between volume and area. Notice the differences between the two formulas:
surface area is a two dimensional measurement since we have multiplied two
lengths together, and volume is the product of an area and a length which
creates a three dimensional measurement.
We need to present all this material to our students before we begin
to investigate these problems using technology. The first day of this lesson
should be this introduction. We need to make sure that the concepts presented
above are understood. Students can easily multiply two numbers together
with their calculators and at the same time have no idea what it is what
they were computing. ASK QUESTIONS THAT EMPHASIZE THE MATHEMATICAL CONCEPTS
OF AREA AND VOLUME RATHER THAN THE COMPUTATIONS!
HOMEWORK : If the cylinder cut out was given as a presentation and
not an activity than have the students create the "net" or cut
outs needed to create the cylinder and fold them as a class at the beginning
of the next class. Assign problems from the text you are using that call
for the student to find surface areas and volumes of right cylinders and
rectangular solids. The following is a homework hand out that could replace
or accompany the work from your text.
CYLINDERS: SURFACE AREAS AND VOLUMES
FORMULAS:
1)SURFACE AREA OF A RIGHT CYLINDER = (height of cylinder ) X (perimeter
of base of cylinder) + (area of base or bases)
2) VOLUME OF A RIGHT CYLINDER = (height of cylinder ) X (area of base of
cylinder)
PROBLEMS:
1) What measures the union of the boundary of an three dimensional object
and the space within the boundary, surface are or volume?
2) What is the formula for lateral area of a right cylinder?
3) A right cylinder has a radius of R and a height of H. What are the formulas
for surface area and volume of a right cylinder in terms of radius and height?
4) Find the surface areas and volumes of each of the cylinders with the
given characteristics:
a) a cylinder with radius 9 feet and a height of 6 feet?
b) a cylinder with a diameter of 6 feet and a radius of 9 feet?
c) a cylinder with radius 9 yards and height of 15 yards?
d) a cylinder with diameter 15 yards and height of 20 feet?
e) which of the cylinders above will hold the most water if filled to capacity?
5) sketch the "net" of a right cylinder.
a) Can you write the formulas that can be used to find surface area and
volume of our sketch using only one variable? hint: the radius and height
are dependent on each other in this situation!!!!
6) If the city needs to build a water tower that is the shape of a right
cylinder that will hold 100,000 cubic feet of water, what are possible dimensions
of the new water tower? (I am looking for the height and radius of our water
tower.)
7) How can we minimize the surface area of our water tower and still hold
the 100,000 cubic feet of water?
The follow up to this exercise sheet should be done in the computer
lab or at least the demonstrations of technology should be presented to
the class!
We can investigate each of the problems using GSP. A sketch of each "net"
should be done so that the radius of our base or length and height of our
box can be adjusted. If the computers are out of reach , overheads can be
made from these sketches and used in the classroom until the computer lab
can be used. The following are examples of overheads taken from the cylinder
sketch:
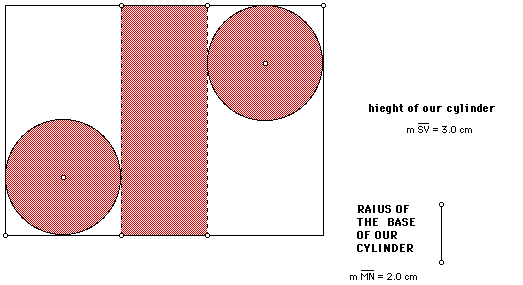

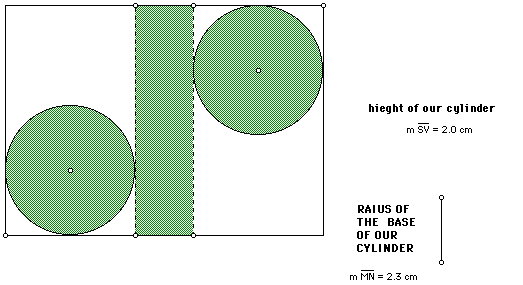
If you would kike to access the GSP sketch that created these examples CLICK
HERE !!!
We can also use GSP to create three dimensional objects that can manipulated
by "parent segments" that will calculate surface areas and volumes.
These types of sketches are interesting to play with, but probably a bit
difficult for a high school student to create on his or her own.
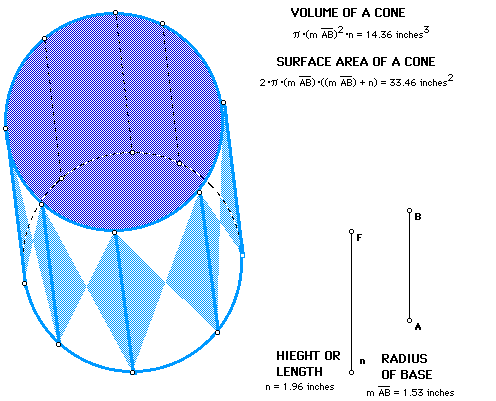
If you would like to access this GSP cylinder click
HERE!!
We can use this exercise to teach kids how to use GSP and how to create
sketches that are of use. This will take time and the students will need
play with the program in order to realize some comfort with and understanding
of Geometer's Sketch Pad.
Another possible lab exploration that will maximize the technology our students
see is to set up the lab with GSP on a few computers, Algebra expressor
on a few computers, and a spread sheet program on other computers. We can
let split the class into three group and let each group investigate each
program. If the class has a set of graphing calculator that can be taken
into the computer lab the students could graph the equations and check their
work with Algebra expressor. The same type of exercise could be done with
the TABLE function that is part of most graphing calculators (TI-82) and
the spread sheet program.
If the computer lab is unavailable these problems are great exercises for
the graphing calculator that can be supported by a computer or not, depending
on the availability of computers.
HOMEWORK: Have your students create a problem that is similar to the box
/ cylinder problem that is to be solved in class the next day, or the next
day in the computer lab. Have them also create and solve a word problem
that is similar to my water tower problem.
SUMMARY:
This is a two to three day lesson that focuses on the surface area and volume
of right cylinders. We have made the assumption that our students have a
general understanding of algebra and have explored the "box problem".
I envision this lesson being useful in a college bound geometry class or
as a closing section that focuses on the connections between different disciplines
within mathematics. The lesson grants the educator room for changes that
are inevitable, since every class and teacher is different. The use of technology
I think is a must. At the very least the graphing calculator needs to be
involved if the students are going to realize all the connections between
geometry, algebra, and real life.
I have included examples of the sketches, the Algebra Xpresser file, and
the spreadsheet that I suggested.
If you would like to access the Algebra Xpresser to see a graph of the "cylinder
problem"
CLICK HERE!!!
If you would like to see the Excell spreadsheet I used to solve the "cylinder
problem "
CLICK HERE!!!
OBJECTIVES:
1) We want our students to have a basic understanding of the concepts of
SURFACE AREA AND VOLUME.
2) We want our students to be able to recognize a right cylinder when the
see one.
3) We want our students to understand how the formulas for surface area
and volume of a right cylinder are derived. I also hope the connections
between other shapes and their surface areas and volumes such as squares,
rectangles, and spheres can be incorporated.
4) Introduce a real world problem and show the students that computers and
technology are an invaluable resource.





