Investigational Essay
Triangle Centers
We will look at four different centers of triangles. These
are the centroid, circumcenter, incenter and orthocenter. I have presented
examples and definitions for each of the centers.
Centroid
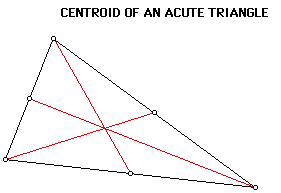
Definition: The centroid of a triangle is the intersection of the three
medians of the triangle. A median is the line that passes through the mid-point
of one side of the triangle and the opposite vertex. Here is an example
of a centroid.
CLICK HERE to
see an example of the centroid of an obtuse triangle!!!
CLICK HERE
to see an example of the centroid of an right triangle!!!
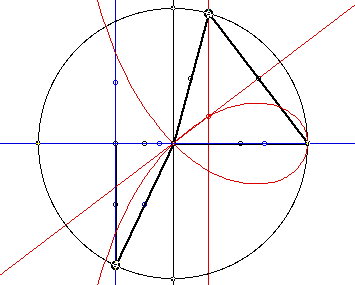
I
have used Geometer's sketch pad to look at the path of the centroid as our
triangle moves from 0 degrees to 180 degrees. I have also constructed a
right triangle that will rotate around the unit circle. I have traced the
centroid of this triangle in hopes of seeing some characteristics of right
triangle centroids.
CLICK HERE if you would like
access to the GSP file I used to create the picture below!!!

Circumcenter
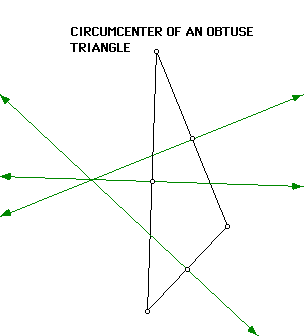
Definition: The circumcenter of a triangle is the intersection
of the three perpendicular bisectors of the triangle. A perpendicular bisectors
is the line that passes through the mid-point of one side of the triangle
and is perpendicular to that side. Here is an example of a circumcenter.
CLICK HERE
to see an example of the circumcenter of an acute triangle!!!
CLICK HERE to see an example
of the circumcenter of an right triangle!!!
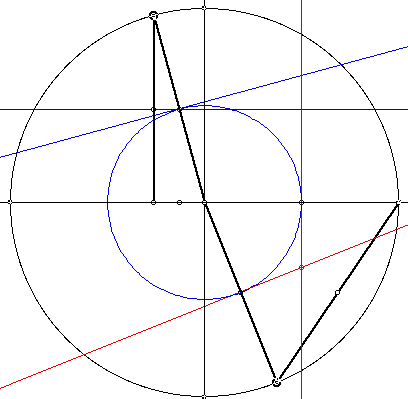
I have used Geometer's sketch pad to look at the path of
the circumcenter as our triangle moves from 0 degrees to 180 degrees. I
have also constructed a right triangle that will rotate around the unit
circle. I have traced the circumcenter of this triangle in hopes of seeing
some characteristics of right triangle
circumcenters.
CLICK HERE if you would
like access to the GSP file I used to create the picture below!!!
Incenter
Definition: The Incenter of a triangle is the intersection of
the three angle bisectors of the triangle. A angle bisectors is the line
that passes through a vertex an divides that interior angle of the triangle
in half. Here is an example of an incenter.

CLICK HERE to
see an example of the incenter of an acute triangle!!!
CLICK HERE to see an example of
the incenter of an obtuse triangle!!!
I have used Geometer's sketch pad to look at the path of
the incenter, as our triangle moves from 0 degrees to 180 degrees. I have
also constructed a right triangle that will rotate around the unit circle.
I have traced the circumcenter of this triangle in hopes of seeing some
characteristics of right triangle incenters.
CLICK HERE if you would like
access to the GSP file I used to create the picture below!!!
Orthocenters
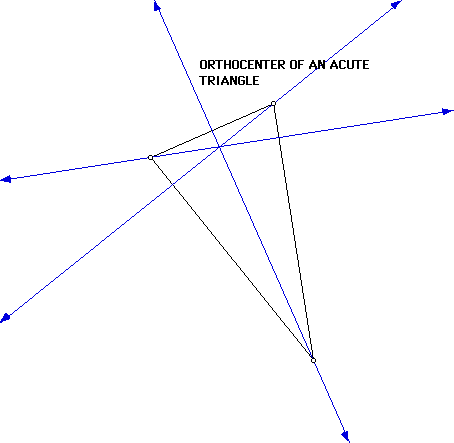
Definition: The orthocenter of a triangle is the intersection
of the three altitudes of the triangle. An altitude is the line that passes
through a vertex and is perpendicular to the opposite side of the triangle.
Here is an example of an orthocenter.
CLICK HERE
to see an example of the orthocenter of an obtuse triangle!!!
CLICK HERE to see an example
of the orthocenter of an right triangle!!!
I have used Geometer's
sketch pad to look at the path of the orthocenter, as our triangle moves
from 0 degrees to 180 degrees. I have also constructed a right triangle
that will rotate around the unit circle. I have traced the orthocenter of
this triangle in hopes of seeing some characteristics of right triangle
orthocenters.
CLICK HERE if you would
like access to the GSP file I used to create the picture below!!!