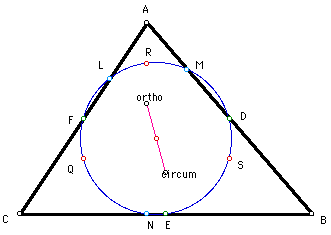

With exploration one is quickly able to see that the area of the nine
point circle has a constant ratio to the circumcircle of triangle ABC. The
proof of this is very straight forward.
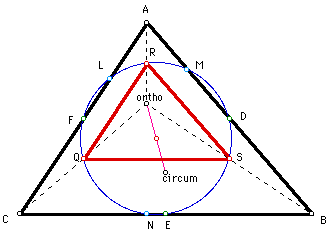
If we call the orthocenter point O then we can see the three triangles
AOC, BOC, and AOB. Notice the red segments joining points Q, S, and R ,
the midpoints of CO, AO, and BO. This makes the red segments one half the
length of the corresponding sides of triangle ABC. Thus by the Side-side-side
Similarity Theorem the red triangle QRS is similar to the black triangle
ABC, with a ratio of 1:2. Therefore the ratio of the area of triangle QRS
to triangle ABC is 1:4 as the display below clearly shows.
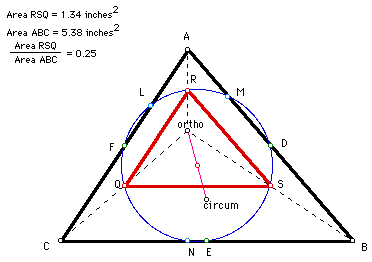
Now that we have clearly shown that the areas have a ratio of 1:4 we
can then look at the radii of the nine point circle and the circumcircle.
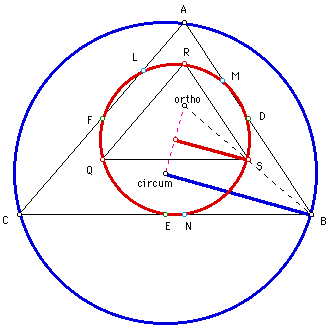
The heavy red segment is the radius of the nine point circle and the
heavy blue segment is the radius of the circumcircle. We look at the triangle
created by the orthocenter, circumcenter, and point B, noticing that point
S is the mid point of line segment OB; also the center of the nine point
circle is the midpoint of the line segment connecting the circumcenter and
the orthocenter. This shows the radius of the nine point circle to be one
half the length of the radius of the circumcircle. Therefore the ratio of
the area of the nine point circle to the area of the circumcircle is again
1:4 as the display below clearly shows.
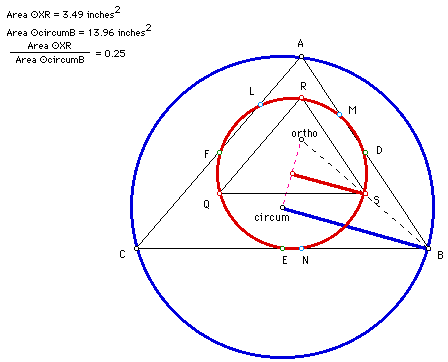
This proves that the area of the nine point circle of a given triangle
is one-fourth the the area of its circumcircle.
To see an animation of a nine point circle in motion click
here.
click here to return to home page