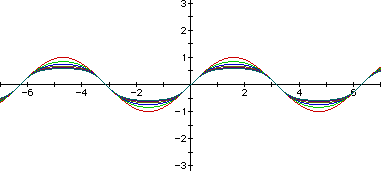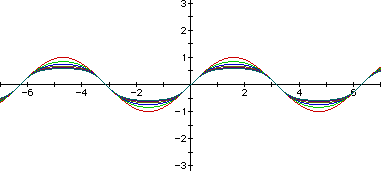A Look at Iterations of Sin(x) and Cos(x)
by
Emily Willis
In this essay we will look at the iterations of the sine and cosine curve.
We will look at two different ways to represent them graphically.
Below we have the graph of y=sin(x) iterated six times: y=sin (x), y=sin(sin
(x)), y=sin(sin(sin (x))), y=sin(sin(sin(sin (x)))), y=sin(sin(sin(sin(sin
(x))))), and y=sin(sin(sin(sin(sin(sin (x)))))).
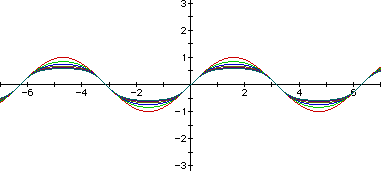
From this graph we see that the sin(x) curve is gradually flattening out.
We can hypothesize that the curve is approaching zero. This graph was done
on Algebra Expresser, but it might be helpful to view this curve produced
on Excel.
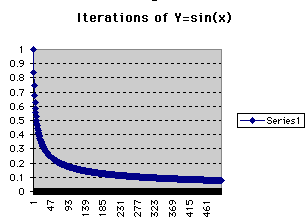
Here we get a better view of what is meant by the curve approaching zero.
We started the curve by taking the sin(1) and then iterated the function
hundreds of times. What kind of conjectures can we draw from this graph?
It might be useful to point out that the sine function had to iterated over
461 times in order to produce this curve. Without technology available it
would have been very difficult to produce such a curve.
Now we will move our attention to the cosine curve. Once again let us look
at the curve produced by Algebra Expresser iterating the cosine function
six times. This is the graph of the following equations: y=cos(x), y=cos(cos(x)),
y=cos(cos(cos(x))), y=cos(cos(cos(cos(x)))), y=cos(cos(cos(cos(cos(x))))),
and y=cos(cos(cos(cos(cos(cos(x)))))).
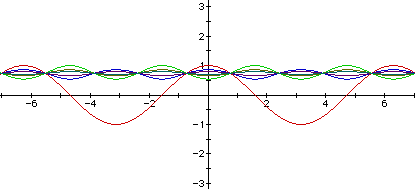
As opposed to the sine curve we see that the cosine curve quickly begins
to approach a value close to one. What is the value? Well, let's look at
what Excel has to offer us.
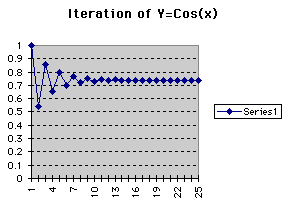
From this graph we get a better idea that the value the cosine interations
approach is somewhere between 7.0 and 7.5. Once again we notice here in
Excel that the cosine function reaches a close approximation much more quickly
than that of the sine curve. Here the function is only iterated a matter
of twenty-five times as opposed to hundreds.
Return to Emily's Home Page