Something Different

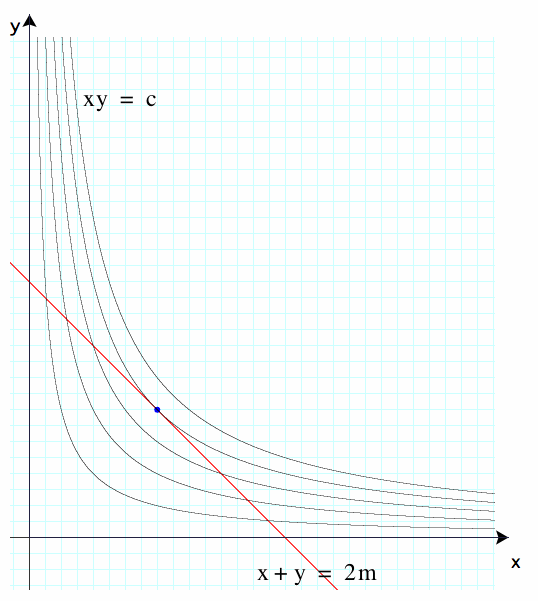
Consider a family of hyperbolas given by xy = c for different values of c. We will look only at the branches of these hyperbolas in the first quadrant -- x and y are both positive.

These curves are symmetric with respect to x and y; each curve is part of a rectangular hyperbola with asymptotes x = 0 and y = 0.

Now, consider the line x + y = 2m graphed on these same axes. The xy = c curve with the greatest value of c having a single point in common with the line is where we have x = y = m, that is, the point (m, m).