

Bridges normally have expansion joints built in so that as the material changes from heat, for example, the change is absorbed without disturbing the surface. The ends are firmly anchored at A and C. Let the bridge be one mile (5280 ft) long. If the coefficient of expansion is (1/2640) the bridge surface would increase in length by 2 ft. Consider that the expansion occurs in the shape of an arc of a circle.
Discussion: What is your intuition? Would a person 6 ft tall still be able to see a person 6 ft tall at the other end of the bridge at maximum expansion?
Question: How high would the center of the bridge be at maximum expansion?
Will this height be considerably less than the height for the hinged example?
The arc and chord will belong to some circle with radius r. We examine a sector.
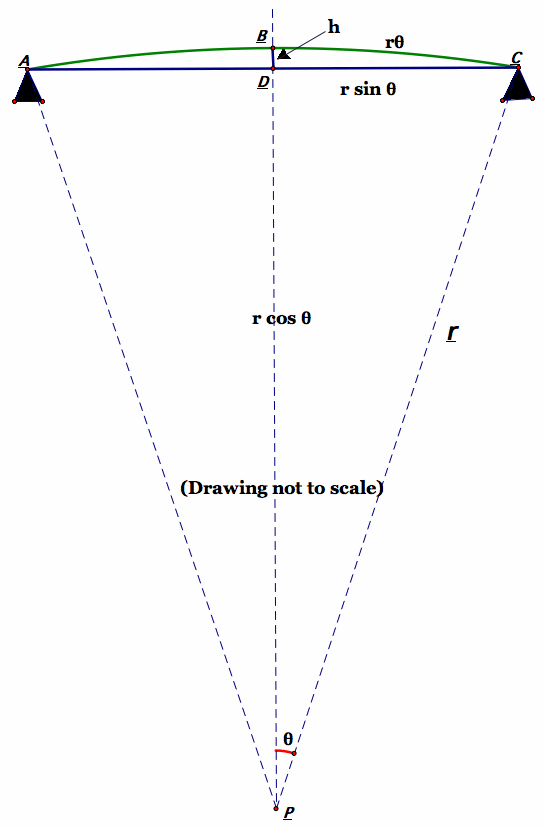
Need a HINT for solving the pair of equations?
Return to the EMAT 4600/6600 page
Note: More sophisticated and accurate models of the bridge expansion would yield a curve that is not the arc of the circle. However, the height of the arc of a circle is close to the height of a more sophisticated and accurate curve, to within a few percentage points.