
Brahmagupta's Formula

where s is the semiperimeter.
Given:
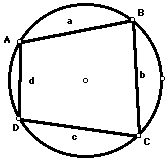
Draw chord AC. Extend AB and CD so they meet at point P.
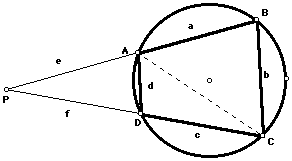
Angle ADC and Angle ABC subtend the same chord AC from the two arcs
of the circle. Therefore they are supplementary. Angle ADP is supplementary
to Angle ADC. So
Triangle PBC and Triangle PDA are similar. The ratio of similarity
is
Area of Triangle PDA = ![]() * Area of Triangle PBC
* Area of Triangle PBC
Area ABCD = Area of Triangle PBC - Area of Triangle PDA
Let A = Area of quadrilateral ABCD and T = Area of Triangle PBC.
Let PA = e and PD = f. Applying Heron's Formula, the area of triangle
PBC is
Therefore,
(Note: We have used s at this point for the semiperimeter of the TRIANGLE.
In what follows, we will substitute for s, e, and f in terms of a, b, c,
and d. Eventually we will return to the use of s to represent the semiperimeter
of the quadrilateral. )
1. First, we want a substitution for e in terms of a, b, c, and d.
2. Next, we want a substitution for f in terms of a, b, c, and d.
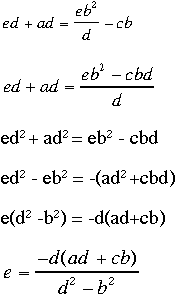
3. Now we will make some substitutions in the formulas for the triangle.
4. Now evaluate s(s - (e + a)
5. Likewise, we now evaluate s - (f + c) in terms of a, b, c, and d.
6. Now, we evaluate (s - b)
7. Now we are ready to evaluate the Area of the quadrilateral in terms of a, b, c, d.
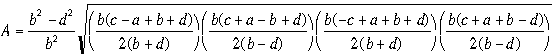
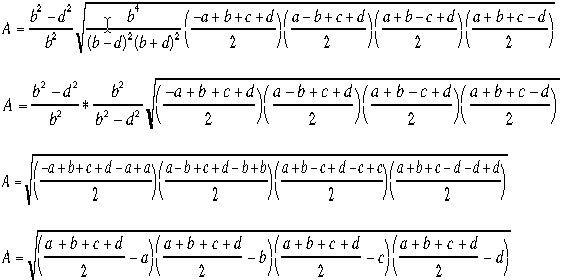
where s is the semiperimeter of the cyclic quadrilateral
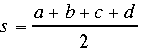
Click here to see a
Microsoft Word 6.0 document for this proof of Brahmagupta's Formula.
Return to Tammy Brooks's Homepage