
Napoleon's Theorem
by Kala Fischbein and Tammy Brooks
Given any triangle, we can construct equilateral triangles on the sides
of each leg. In these equilateral triangles, we can then find the centers:
centroid, orthocenter, circumcenter, and incenter. Each of these centers
is in the same location because the triangles are equilateral. After the
centers have been located, we connect them thus forming Napoleon's Triangle.
Construction of Napoleon's Triangle.
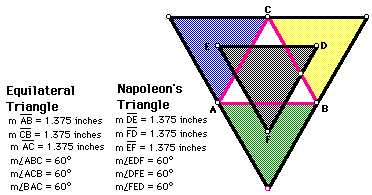
Napoleon's Triangle is the grey triangle. Notice that it is also an
equilateral triangle.
Napoleon's Triangle appears to be congruent to the original equilateral
triangle ABC by the SSS postulate. Now, let's see what happens when our
original triangle is a right triangle.
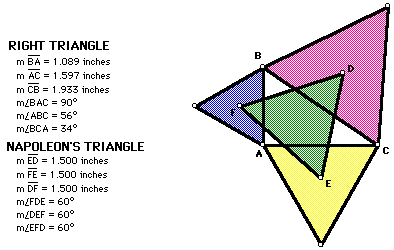
The green triangle, which is Napoleon's Triangle, is still an equilateral
triangle.
Let us explore when the original triangle is an isosceles triangle.
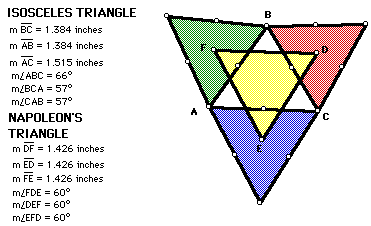
Notice that the yellow triangle represents Napoleon's Triangle which
remains an equilateral triangle.
After exploring all of the special types of triangles, what happens when
we have a scalene or general triangle?
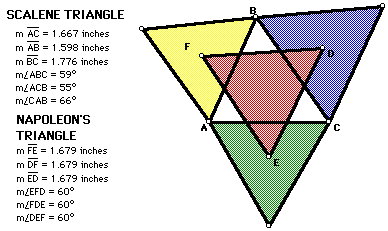
Again, notice that Napoleon's Triangle, the red triangle, is still equilateral
no matter which type of triangle is used for the original triangle.
In conclusion, when finding Napoleon's Triangle we know that by connecting
the centers of the outlying triangles we will construct an equilateral triangle.
To look at some GSP sketches of the above explorations click
here.
Return to Kala's
EMT 525 Home Page





