PROBLEM: Four Dogs

Click here for a statement of the problem.

Discussion/ Solution?:

Four dogs, A, B, C, and D, are located at the vertices of a square. They start to run at the same time and at the same speed. A runs toward B, B runs toward C, C runs toward D, and D runs toward A.

Eventually they all meet in the center of the square? Why?

The dogs will meet at the center of the square because they each follow along an arc of a circle that passes through the center of the square and two vertices of the square.

Each path is actually one-fourth of the circle it follows. Let 2s represent the length of the side of the square. The radius of each circle is s. So the circumference of each circle is C = 2pr = 2ps. Thus, each dog travels a distance of d = (2ps)/4 = ps/2 .

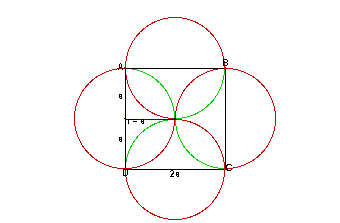
Each dog begins his journey at the corners of the square. So each dog begins at the intersection of a vertex and a diagonal. The path of each dog doesn't cross the diagonals again until they meet in the middle of the square.

Click here for an animation of the dog chase.

Return to Susie Lanier's Class Page.