Teaching Linear Functions Within A Geometric Perspective
An Essay
Written for: Dr. J. Wilson
Ma 669, Winter Quarter
Written by: Sandra M. McAdams
In exploring various ways that my students might begin to understand linear functions better I thought I might depart from the usual approach to graphing lines and simply using rote methods for finding slope and intercept. I have found that with an approach that implements technology the students not only are more interested initially they also seem to gain a much deeper understanding of how linear functions behave. Often when teachers teach about linear functions we begin by graphing relationships from what our students call T-tables i.e. a table of values determined by choosing various values for x and determining the corresponding y value. Of course some students become so adept at this method of graphing a line that we can scarcely pry them away from plugging in points for ever. This essay gives a different approach to introducing linear functions using the technology of the computer and the software called Geometer's Sketch Pad (GSP). I like to use the graphing calculator while in the classroom to help students understand various relationships that are linear in nature. The graphing calculators allow us to graph scatter plots and examine relationships, but the following labs give the students a more dynamic approach and encourage more thought. These labs will help them think about relationships not just rote operations.
In the Addison- Wesley book Secondary Mathematics - Focus on Algebra adopted by Gwinnett County there is an integrated approach to algebra and geometry. This textbook is used to teach primarily freshmen. We begin introducing functional relationships by using tables and asking students to look for patterns and describe the relationship between X and Y for a particular table. I think it would be natural at this point to give them several lab experiments in which they could use GSP. A prerequisite would be a functional knowledge of basic commands on GSP. If they were not familiar with the environment, a few days would be required to help them become obtain a basic knowledge of the program. It is very frustrating to try to teach mathematics in the context of teaching a computer environment. The students become discouraged with the syntax, etc. and are then unable to concentrate on the mathematics which you hope to convey. I would strongly urge anyone to bring their students up to a minimal level of functioning within GSP before using the following labs. This lab approach not only serves to give them a minimal competency in graphing and determining relationships, it also enhances their concept of independent and dependent variables and allows them to focus on relationships.
GSP Lab
Algebra & Geometry
Objective: Construct a path of motion given constraint of being equidistant from some point.
Part 1
Place two points arbitrarily on the screen. Label them A and B. Imagine a point C which moves along a path that will always be equidistant from points A and B.
A. Construct the path on which C would travel. Describe the construction.
B. Use the measure menu to justify the statement that AC = BC at several points along this path. You may use the animate button or move the point C manually.
C. Is there a special mathematical name given for this path?
Click here for GSP
Part 2
A. Construct two perpendicular lines.
B. Construct the path of some point P that moves in such a way that it will always be equidistant from the two lines.
C. Describe the construction. Can this construction be done in more than one way? If so, describe a second construction.
D. Use the measure menu to justify that you have in fact chosen the right path.
E. How is Part 2 of this lab like Part 1? How is it different?
Click here for GSP
After the lab the homework would follow up on finding patterns and writing relationships that the students see. The next lab will extend the idea of being equidistant from some arbitrary point or line to being equidistant from the X and Y axes.
GSP Lab
Algebra & Geometry
Objective: Construct a path of motion using the coordinate plane given constraints of equidistance or constant ratios.
A. Turn on GSP grid. Construct the path of some point P ( X,Y) in the plane that moves in such a way that it is always equidistant from the X and Y axes.
B. Use the measure menu to verify your path. Give several measurements.
C. What would the relationship be between the X-coordinate and the Y-coordinate of the moving point?
D. Make a table of values that would demonstrate this relationship.
E. Is there only one path that would satisfy this condition? If there is more than one, construct the other path(s) and then describe the relationship of the X- coordinate and the Y-coordinate on this new path.
Click here for GSP
Hopefully at this time the student is beginning to see lines as paths of motion. We are now ready to introduce lines with ratios other than one to one.
GSP Lab
Algebra & Geometry
Objective: Construct paths of motion using the coordinate plane with distances from the axes given as constant ratios.
A. Turn on GSP grid. Construct point P (X,Y) so that it is three times as far from the X axis as it is from the Y axis.
B. Construct the path of some point P (X,Y) so that it moves in such as way that it is always three times as far from the X axis as from the Y axis.
C. Make a table of values that would demonstrate this relationship.
D. Verify that this relationship exists on your diagram by using the measure menu. Verify this for at least three points along this path.
E. Find the relationship between the X and Y coordinates of the variable point P. Using your text tool write this in equation form. Print.
Click here for GSP
Click here for diagram
GSP Lab
Algebra & Geometry
Objective: Introducing positive and negative ratios into line equations.
A. Turn on GSP grid. Construct the path of some point P(X,Y) which moves in such a way that the ratio of the distance from the X axis to the distance from the Y axis is always 4 to 3.
B. Select at least three points along the path and verify that the ratio for each of these distances remains constant.
C. What is the relationship between the X and the Y coordinates?
D. Give an equation of a line that is the path of P.
E. Repeat steps A - D for the ratio 5 to -2.
F. If a variable point P(X,Y) moves in such a way that the ratio of Y to X is 3 to 5, find a relationship between the X and the Y coordinates.
E. Use the relationship from part F to write a line equation for the path of motion.
Following these labs a discussion of families of lines could take place, and after ample practice with GSP and on paper this would naturally lead into translations of those families.
GSP Lab
Algebra & Geometry
Objective: Discuss vertical translations of lines.
A. Graph Y = X using the ideas from previous labs.
B. How did we determine this path?
C. How will this graph look if it is translated vertically 4 units?
D. What will be the new relationship between X and Y ?
E. Write the equation of the line.
F. Draw two other translations of this line, then give their respective equations.
G. Given the equation Y = .5X - 1 translate it to the origin and discuss the ratio of the distances from the X and Y axes.
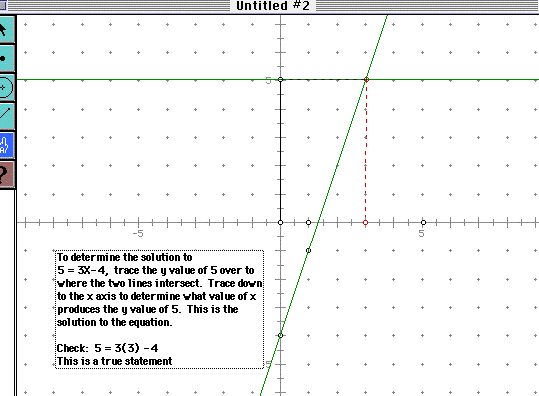
Students will then be prepared for applications of linear functions in real world problems and several days of real world applications, more pattern finding and writing equations from applications should follow. A discussion about the distances from the X and Y axes could introduce the concept of slope and graphing using slope intercept form of an equation. Along with graphing I would ask students to interpret their graphs as well as solve equations using graphs. I have found that asking them to interpret solutions from graphs gives them more insight into what the graph really represents, and I get a greater sense of what they do and do not understand. For example. Start with a discussion of the graph of y = 3X -4, then use various values of y to allow them to solve. Using 5 = 3X -4 have student draw a horizontal line at y = 5 then locate the intersection. Determine the value of x that produces this value of y. Alternately you might have a student use software or a graphing calculator to do the same thing.
See diagram from GSP below.

Click here for a GSP sketch .
If the student has used systems prior to this they will understand this in the context of solving a system. In the normal freshman course however, most students are not familiar with solving systems until after learning about linear functions. In this case I recommend that they simply use the idea of tracing to the desired y value and then trace down to the x axis to find the corresponding x value. This can also launch a nice discussion of independent and dependent variables.
I think by approaching lines in this way students will have a greater understanding of how the equations and their graphs are related. I know that for myself integrating the algebra and its geometrical interpretations always broadens my perspective, and I hope it will be beneficial to my students as well.