Assignment One
Ma 668, Fall Semester 1997
Written for Dr. J. Wilson
Written by Sandra McAdams
Operations With Linear Functions - A Geometric Interpretation
This discussion will describe the geometric interpretation of simple
algebraic manipulation that is typical of an Algebra I class. A prerequisite
to this lab would be knowledge of how to graph a linear function, how to
combine like terms, how to multiply polynomials and how to interpret function
notation. I will use software titled xFunctions 2.2, however there are many
software packages such as MacNumerics or Algebra Expressor that would help
a student discover the relationships in this article. Furthermore a graphing
calculator would probably be more accessible to many classes, and it provides
an excellent opportunity for large class groups who do not have computer
labs. Also it is my experience that the simple syntax on the graphing calculator
is easier for students to learn.
Often in the first algebra course a student is asked to do many manipulations
with variables, however, even the most capable students are sometimes not
introduced to the geometry behind the manipulation. This discussion will
attempt to show how the various operations performed effect the original
function. Further it should familiarize the student with some of the available
software.
Let F(x) = 5 x + 2 and G(x) = -3 x - 5
We will look at graphs of a new function H(x) beginning with the sum, i.e.
H(x) = F(x) + G(x).
To introduce the student to xFunctions 2.2 begin by opening the program,
then go to Utilities < Multigraph. This allows the student to graph several
graphs on the same axes. Enter the function as a function of x in the edit
box at the bottom of the page. Be sure to set y maximum and minimum values.
Click on Graph it and discuss the observations made. Note below there is
a graph of the sum of the linear functions and an example of what you can
expect on the screen.
F(x) + G(x) = H(x) = 2 x - 3
(Pink + Blue = Green)
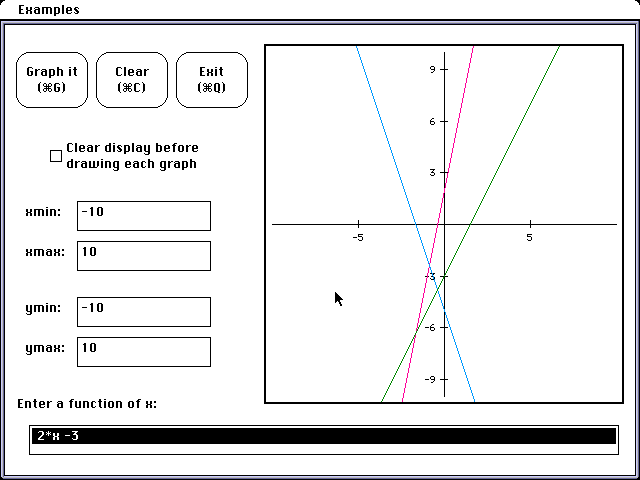
A student might be asked to determine if the sum of two lines would always
generate another line. The student could also use the program to show point
by point addition for a selected number of points from each line.
The next question posed could be what does the product of two lines produce.
Of course this leads naturally to the degree of the new equation. The student
could again use xFunctions 2.2 to produce several examples. Once the functions
are typed into the edit line the student can simply erase the operation
symbol and replace it with a new operation One such example follows.
H(x) = F(x) * G(x)
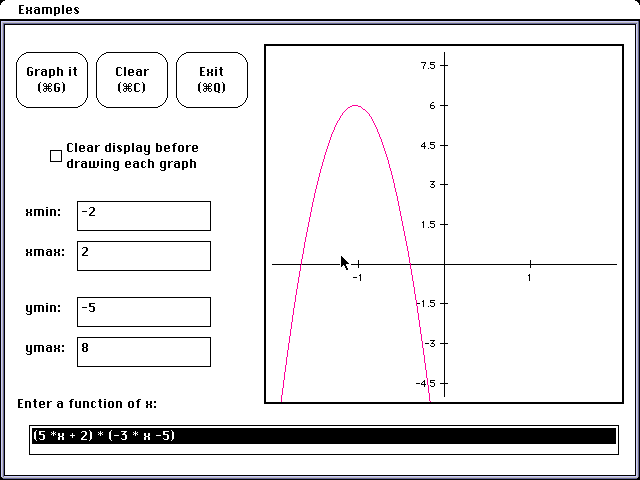
This could lead then to a discussion of quadratics, how to graph them, what
are some natural applications etc. One disadvantage to the xFunctions2.2
software is that it does not allow a student to trace on the graph. MacNumerics
is an excellent program for tracing values and the discussion of how to
locate the vertex or maximum of this curve by tracing. Its disadvantage
is that MacNumerics is heavy on notation and would probably be better suited
for more advanced students. Following the discussion on multiplying two
lines it would be natural to ask what happens when we multiply to quadratics.
A discussion of how the degree would be affected and how this is related
to the changes in the graph would be appropriate for the more advanced algebra
course.
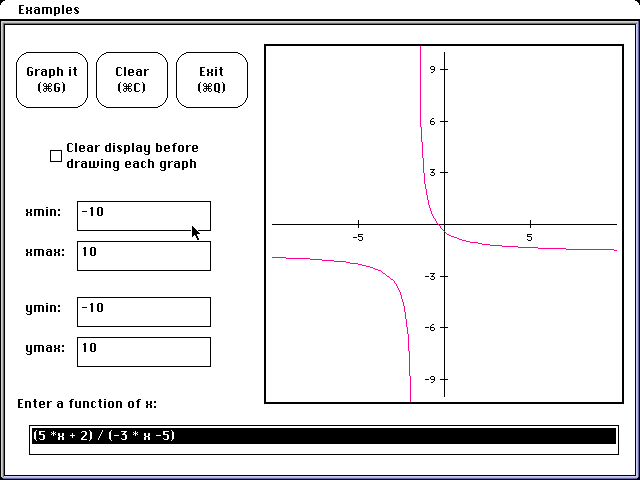
Following the same format the student could discover the division of two
linear equations leads to a rational function, the graph of which is a hyperbola.
Algebra one students seem particularly interested in this graph because
it is not familiar to them. The technology allows us to graph hyperbolas
without the tediousness of plotting many points. It is important, however
that the student be able to plot points and understand why the graph behaves
the way it does. Without using the terminology asymptotes can be discussed.
In particular as one discusses the domain and range of a function the rational
function helps to clarify what we mean when we say that x cannot be a certain
value. This function helps the teacher differentiate between the students
who understand domain and range and those who do not. This can lead to a
nice discussion about division by zero and undefined quantities. Of course
more advanced students could find vertical and horizontal asymptotes, but
even the novice understands the vertical asymptote and how this relates
to undefined quantities for the equation.
H(x) = F(x) / G(x)
Finally students could examine the effects of composing two functions. Most
Algebra II students have difficulty with the composition of two functions.
I think this could also be an excellent place to discuss domain and range
of a function. The student composing two lines would discover that a new
line was formed and after several examples they could hopefully generalize
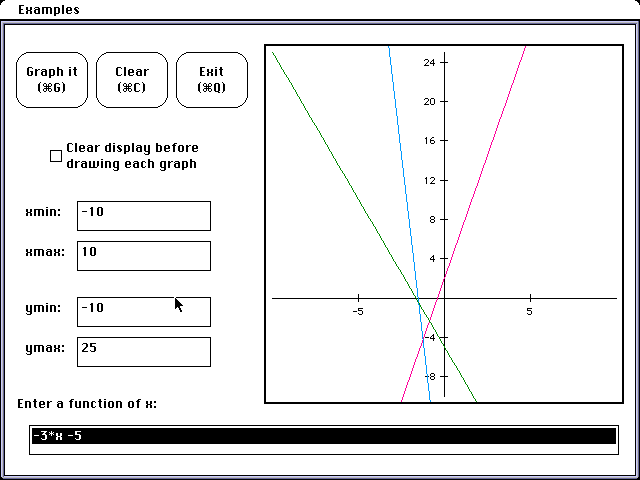
or make conjectures about translations and stretches. For our specific case
when we look at F ( G(x)) the graph is stretched by a factor of 5 and translated
2 units up. This could be approached as a mapping of individual points to
show how the stretch should occur and then the translation. This could also
be a nice application of the order of operations. For example: F(G(x)) =
5 ( -3x-5) + 2 which simplified is -15x -23, If however we add 2 before
we stretch then the expression becomes -3x -3 which is -15x -15 once it
is stretched. This could demonstrate how the sequence of events does make
a difference. To stretch and then translate is different than to translate
and then stretch. This seems harder to see with quadratic functions which
we typically use when teaching stretches and shrinks of functions in Algebra
II.
Below is a graph of the original lines and the composition. It would of
course follow that G(F(x)) is a completely different graph and graphing
these would help students to see the difference. Additionally when graphing
using Xfunctions 2.2 the student has to replace the x with the expression
thereby reinforcing the replacement of a domain. One could also extend the
students knowledge by using compositions of lines and quadratics or lines
and sinusoidal functions.
F(G(x)) = -15X -23
RETURN TO HOME PAGE



