In this exploration we will look at parametric curves. The word parameter means a variable used to describe the general form of a set of equations. The two equations give the x and y coordinates of a moving object at time t. The two equations are called a set or pair of parametric equations of the curve and the variable t is called the parameter.

We will begin our exploration with a sketch of the curve with parametric equations

and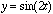

If we were going to graph these by hand we would begin by filling out a table of values. Fortunately we have technology to do the calculating for us, but when students begin to look at these curves there is a place for plotting points and realizing the movement that is taking place. To find the Cartesian equation of the curve we realize that cos (t) = x and therefore

sin(t ) = Then using trig identities and the equation y = 2 sin (t) we have: which when substituted in the equation becomes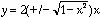 and by simplifying we have . The graph below shows this type of curve.



 

We will continue our exploration by holding a constant and allowing b to vary in the parametic equations x = cos (a t) and y = sin (b t). Through several examples we will begin to see a pattern.

Observe: x = cos(t)

y = sin (3 t)

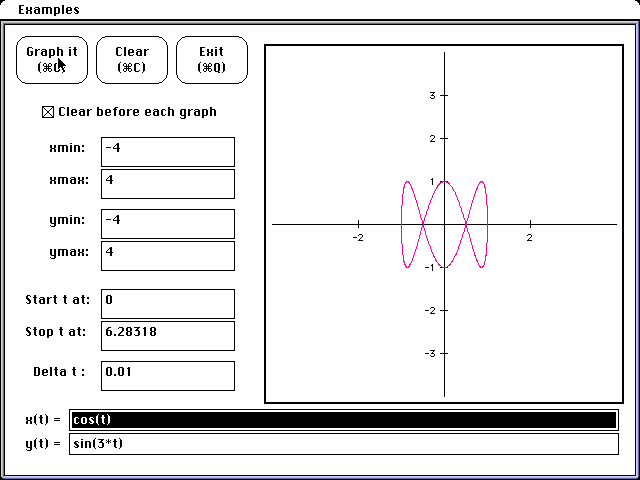
Following with one more example :

x = cost (t)

y = sin ( 4 t )

 



It is apparent that the amplitude or height of the curve does not seem to change. It ranges from 1 to -1 consistently. What does appear to change is the period of the function. There are 2 loops in y = sin( 2 t ), three loops in y = sin (3 t) and so on. We could predict then that the change in b produces a change in the period and will produce b loops along the x axis.

Contrast with that the following diagrams. We will now hold b constant and allow a to vary. An interesting thing happens. It seems to be related to whether the a term is even or odd. Example:

x = cos (2 t) , y = sin (t)



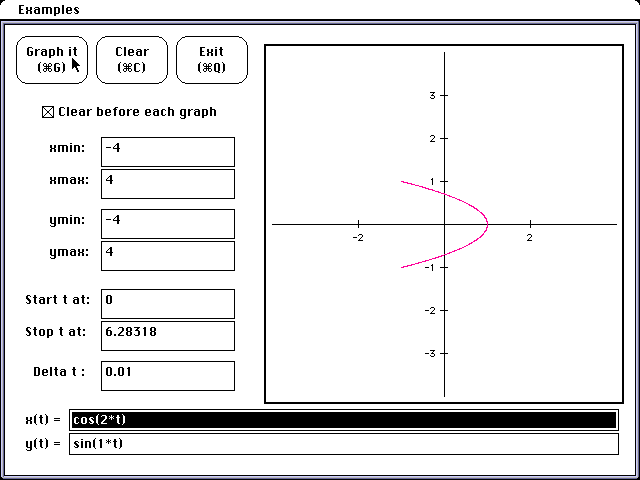
Note what appears to happen when a is an odd number as opposed to an even. We will next look at two cases where we can compare a is odd in example 2; x = cos( 3 t) , y = sin (t ) and then a is even in example 3; x = cos (4 t), y = sin (t).





After drawing several of these I have come to the conclusion that when a is even there is an open curve. However, when a is odd there is a closed curve with a loops completed along the y axis.

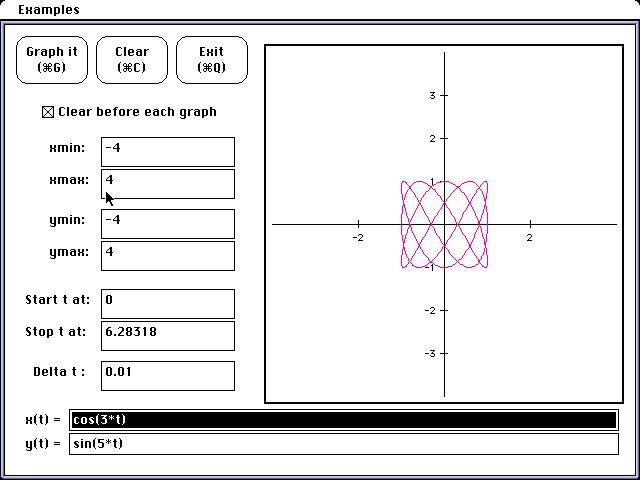
Finally I would like to look at a more complex figure.It is called a Lissajous figure. Lissajous figures are used by radio engineers in frequency and phase measurements of wave motion. Notice the parametric equation for this curve is much simpler than its Cartesian equation.



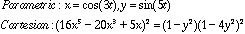
The graph is extremely interesting.



RETURN TO SANDY'S HOME PAGE

Click here to return to Final Assignment