This exploration would be appropriate for most Algebra One students. The purpose of the exploration is to find a relationship between the given variables in the general quadratic function below.

The student will discover the geometric changes that are occuring when one variable a, b, or c is allowed to change while the other two remain constant. Good software choices to use for multiple graphs includes MacNumerics, xFunctions, and Graphing Calculator. These graphs allow the student to graph a sequence of graphs to determine how the change in the equation is related to the change in the graph. MacNumerics and xFunctions 2.2 allow a student to overlay graphs on the same axes which is very effective when discussing relative changes. It is not desirable, however, for a student to produce all the graphs at once as they will be unable to make conjectures about each change. I will use MacNumerics and xFunctions 2.2 in my discussion, but there are many other sofware packages that may be appropriate. Certainly a graphing calculator could be used for these same purposes.

The student might begin by keeping b =1 and c = 1 and allowing a to range from 1 to 4.. Open MacNumerics, then General Functions and type in the various equations observing the changes made in the graphs. The limitations to General Functions include the fact that one can only see two graphs at a time and the notation is rather heavy for an algebra one student. The syntax is standard and relatively easy to use and there is an option for creating an assignment which allows the student to show their graphs and make comments. I will demonstrate this option below.



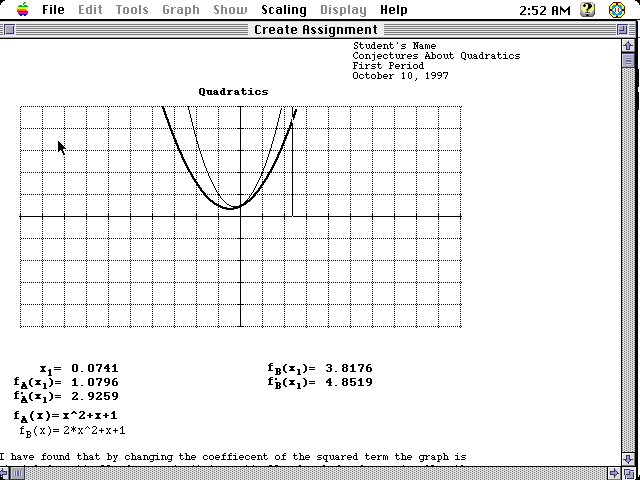
At the bottom of the box you see a place where the student can give their findings. I was unable to show the complete box since this is simply a picture, however open MacNumerics and general functions to see for yourself.Click here for MacNumerics-II

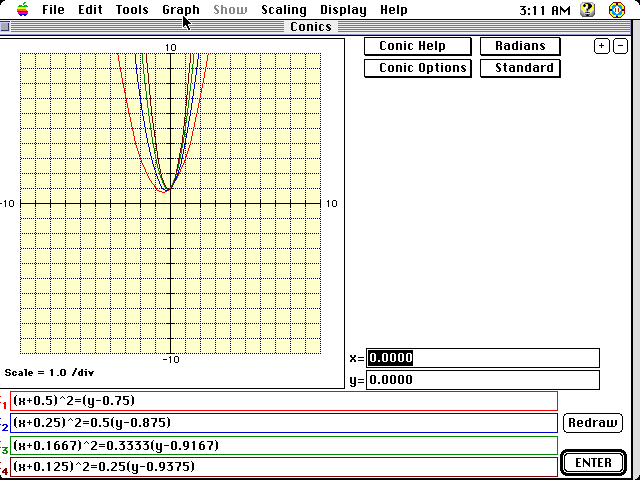
For the more advanced student and the algebra one student that has some experience with function notation and graphs of quadratics the preferred option would be Conic Sections. I will go through an exercise with each of these, however in Conic Sections the initial graph graphs as many as four conics simultaneously. Note that you may enter the conic as a function of x but the program will automatically convert the equation to general or standard form which ever you prefer. Below is the graph obtained when four conics are given as imput.



 

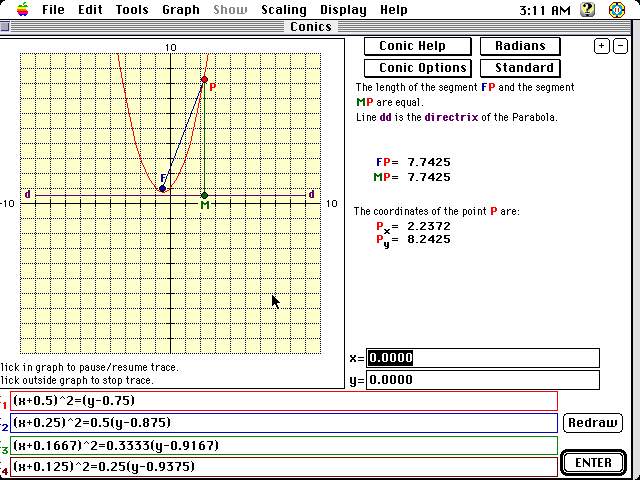
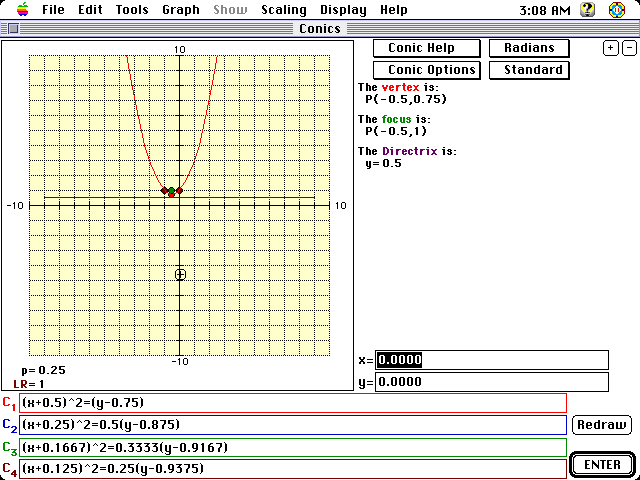
If one uses the options in the program one graph at a time is not only possible, there is an abundant amount of information given about each graph. I will show two of the graphs conic 1 & conic 2. The option I used was conic help.

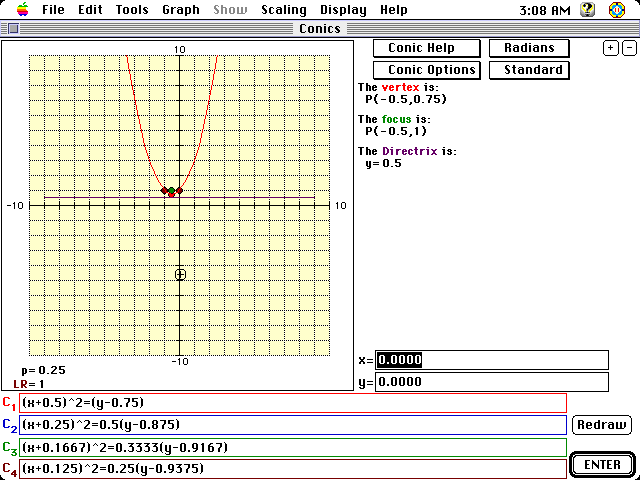
Additionally this program will trace to show by definition the locus of points determined. This allows the teacher to enrich the discussion about quadratics in general.

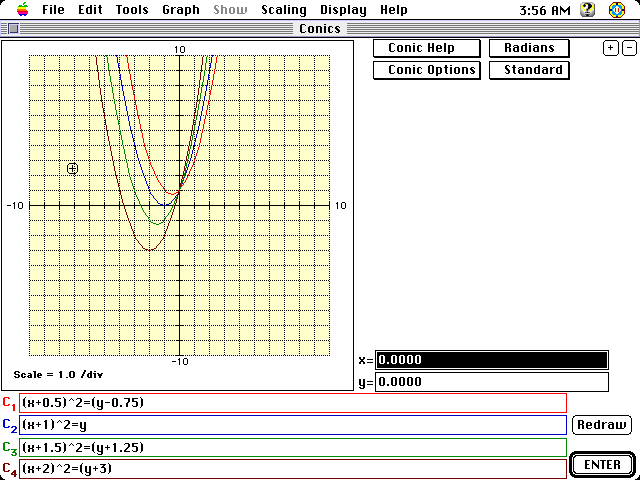
The student could then follow up with holding a constant and allowing b to range from 1 to 4. The conjecture is that changes in b results in a translation of the graph however the y intercepts remain unchanged and the general shape of the graph remains unchanged.




 

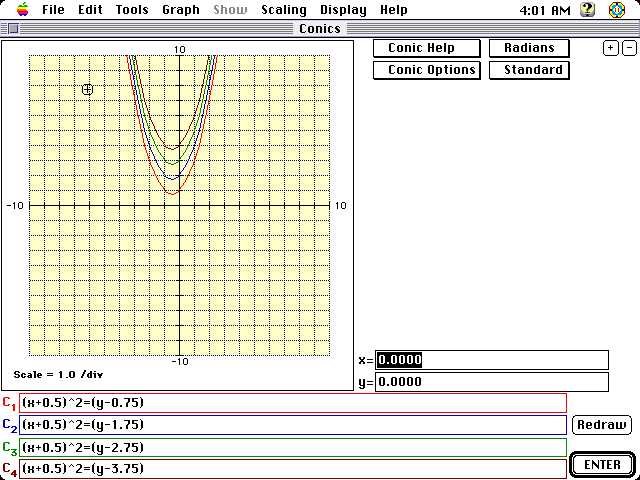
Finally the student could change the constant and keep a = 1 and b = 1 to discover the vertical shift that occurs. With a vertical shift it should be noted that the overall shape of a graph when it is translated remains unchanged. There could be a discussion about the axis of symmetry shared by each of these contrasted with the other changes ie. changes to a and b which did not yield a family which shared a common axis of symmetry.




 

RETURN TO HOME PAGE